Signal Processing Toolbox

時間領域ベースのモデリング

関数lpc、prony、および、stmcbは、与えられた時間領域インパルス応答に近似するディジタル有理伝達関数の係数を求めます。アルゴリズムは、結果のモデルの複雑さや精度により異なります。

線形予測

線形予測モデリングでは、信号の各出力サンプルx(k)が、過去のn個の出力の線形結合である(すなわち、これらの出力から"線形的な予測"が可能である)ということ、ならびに係数がサンプル間で一定であるということを仮定しています。

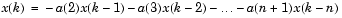
信号xのn次の全極モデルは、つぎのステートメントより得られます。

a = lpc(x,n)

lpcを説明するために、加算的な白色雑音をもつ全極フィルタのインパルス応答であるサンプル信号を作成します。

randn('state',0);
x = impz(1,[1 0.1 0.1 0.1 0.1],10) + randn(10,1)/10;

システムをモデリングする4次の全極フィルタの係数は、つぎのようになります。

a = lpc(x,4)
a = 
        1.0000    0.2574    0.1666    0.1203    0.2598

lpc は、まずxcorrを使って、xの相関関数のバイアス付きの推定値を求め、関数levinsonで実現されているLevinson-Durbinの帰納法を用いてモデル係数aを求めます。Levinson-Durbinの帰納法は、対称トエプリッツ線形方程式を解くための高速のアルゴリズムです。n = 4に対するlpcのアルゴリズムは、つぎのようになります。

r = xcorr(x);
r(1:length(x)-1) = []; % 負の遅れでの相関の除去
a = levinson(r,4)
a = 
     1.0000     0.0395     0.0338     0.0668     0.1264

つぎのように、バイアスのない相関推定値などのさまざまな相関推定値をlevinsonに渡すことにより、他の仮定で線形予測係数を形成することができます。

r = xcorr(x,'unbiased');
r(1:length(x)-1) = []; % 負の遅れでの相関の除去
a = levinson(r,4)
a = 
     1.0000     0.0554     0.0462     0.0974     0.2115

Prony法(ARMAモデリング)

関数pronyは、設定された数の極および零点を用いて信号をモデリングします。データ列xと分子および分母の次数nbおよびnaが与えられると、ステートメント

[b,a] = prony(x,nb,na)

は、そのインパルス応答が列xを近似するIIRフィルタの分子および分母の係数を求めます。

関数 pronyは、Parks and Burrus [3] (226-228 ページ)に記述されている方法を実現します。この方法は、ARモデリングの共分散法を修正したものを用いて分母の係数aを求めた後、生じるフィルタのインパルス応答がxの最初のnb + 1個のサンプルに厳密に一致するように分子の係数bを求めます。このフィルタは必ずしも安定ではありませんが、データ列が、正しい次数の自己回帰移動平均(ARMA)プロセスの場合、係数を正確に回復できる可能性があります。

注意    関数pronyおよびstmcb (次節で説明)は、システム同定用語において、ARXモデルとしてより正確に記述されます。ARMAモデリングでは、入力に雑音のみを仮定していますが、ARXモデリングは、外部入力を仮定しています。pronyおよびstmcbは、入力信号が既知です。これは、pronyの場合はインパルスであり、stmcbの場合には任意データ列です。

3次のIIRフィルタを用いた試験列 x(先のlpcの例題)のモデルは、つぎのようになります。

[b,a] = prony(x,3,3)
b =
     1.1165    -0.2181    -0.6084     0.5369
a =
     1.0000    -0.1619    -0.4765     0.4940

コマンドimpzは、このフィルタのインパスル応答がどの程度、オリジナルのデータ列と一致するかを示します。

format long
[x impz(b,a,10)]
ans =
   0.95674351884718   0.95674351884718
  -0.26655843782381  -0.26655843782381
  -0.07746676935252  -0.07746676935252
  -0.05223235796415  -0.05223235796415
  -0.18754713506815  -0.05726777015121
   0.15348154656430  -0.01204969926150
   0.13986742016521  -0.00057632797226
   0.00609257234067  -0.01271681570687
   0.03349954614087  -0.00407967053863
   0.01086719328209   0.00280486049427

最初の4つのサンプルは正確に一致していることに注目してください。正確に回復する例として、このインパルス応答からButterworthフィルタの係数を回復してみましょう。

[b,a] = butter(4,.2);
h = impz(b,a,26);
[bb,aa] = prony(h,4,4);

この例題を実行してみてください。bb、および、aaは、10^-13の許容範囲でオリジナルのフィルタ係数と一致します。

Steiglitz-McBride法(ARMAモデリング)

stmcbは、近似インパルス応答列x、さらに希望する零点と極の数を与えて、システムb (z )/a (z )の係数を求めます。この関数は、システムの挙動を表わす入出力データ列、あるいは単にシステムのインパルス応答のどちらかを使って、未知のシステムを同定します。デフォルトモードでは、stmcbは、pronyと同様に働きます。

[b,a] = stmcb(x,3,3)
b =
    0.9567   -0.5181    0.5702   -0.5471
a =
    1.0000   -0.2384    0.5234   -0.3065

stmcbは、また、つぎのように与えられた入力列や出力列と 一致するシステムも求めます。

y = filter(1,[1 1],x);  % 出力信号の作成
[b,a] = stmcb(y,x,0,1)
b = 
     1.0000
a =
     1     1

この例題では、xからyを作成するのに用いられたシステムを正確に同定しています。

Steiglitz-McBride法は、フィルタ出力と与えられた出力信号との間の信号の誤差を最小限に抑えようとしながら、分子および分母の係数を同時に解く高速反復アルゴリズムです。このアルゴリズムは、通常急速に収束しますが、モデルの次数が大きすぎる場合には収束しない可能性があります。pronyの場合、同様に、stmcbで得られるフィルタは必ずしも安定しません。これは、その厳密なモデリング手法のためです。

stmcbは、いくつかの重要なアルゴリズムを制御するパラメータの設定を行います。データのモデリングに問題がある場合には、これらのパラメータを変更してください。デフォルトの5回の反復回数を変更し、分母の係数の初期推定値を設定するには、つぎのようにします。

n = 10;            % 反復回数
a = lpc(x,3);      % 分母の初期推定値
[b,a] = stmcb(x,3,3,n,a);

この関数は、ユーザが初期値を設定しない場合には、pronyで作成した全極モデルを初期設定値として使用します。

関数lpc、prony、および、stmcbを比較するために、つぎのようにそれぞれの場合の誤差を計算します。

a1 = lpc(x,3);
[b2,a2] = prony(x,3,3);
[b3,a3] = stmcb(x,3,3);
[x-impz(1,a1,10)  x-impz(b2,a2,10)  x-impz(b3,a3,10)]
ans =
   -0.0433         0   -0.0000
   -0.0240         0    0.0234
   -0.0040         0   -0.0778
   -0.0448   -0.0000    0.0498
   -0.2130   -0.1303   -0.0742
    0.1545    0.1655    0.1270
    0.1426    0.1404    0.1055
    0.0068    0.0188    0.0465
    0.0329    0.0376    0.0530
    0.0108    0.0081   -0.0162
sum(ans.^2)
ans =
    0.0953    0.0659    0.0471

IIRモデルの次数を与えて、モデリング機能を比較すると、上の結果から、この例題の場合にはstmcbが最良であり、ついで、prony、lpcの順となることがわかります。この相対的な性能はモデリング関数の特色を示しています。

パラメトリックモデリング

周波数領域ベースのモデリング