

| Signal Processing Toolbox |   |
ケプストラム解析
ケプストラム解析は、音声処理やイメージ処理などの分野で種々に適用されている非線形信号処理手法です。Signal Processing Toolboxには、ケプストラム解析ための3つの関数を用意しています。
| 演算 |
関数 |
| 複素ケプストラム |
|
| 逆複素ケプストラム |
|
| 実数ケプストラム |
|
データ列xの複素ケプストラムは、xのフーリエ変換の複素自然対数を求め、それを逆フーリエ変換することにより計算されます。
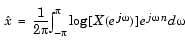
ツールボックスの関数ccepsは、この演算を行って、入力列に対する複素ケプストラムを推定し、入力列と同じ長さの実数列を出力します。
xhat = cceps(x)
複素ケプストラム変換は、ホモモロヒックシステム、すなわち、一般的な重ね合せ規則に従うシステムの理論や適用の中心的なものです。複素ケプストラムおよびホモモロヒック変換に関する事柄については、Oppenheim and Schafer [2] を参照してください。音声処理適用に関する詳細についても記述されています。
つぎに、エコー検出のアプリケーションにccepsを使用してみます。まず、つぎのようにして100 Hzでサンプリングした45 Hzの正弦波を作成します。
t = 0:0.01:1.27; s1 = sin(2*pi*45*t);
信号の立ち上りから0.2秒後に、1/2の振幅をもつ信号のエコーを付加します。
s2 = s1 + 0.5*[zeros(1,20) s1(1:108)];
c = cceps(s2); plot(t,c)
複素ケプストラムは0.2秒の点にエコーを表すピークを示していることに注目してください。
信号xの実数ケプストラムは、場合によっては単にケプストラムと呼ばれるものですが、xのフーリエ変換の大きさの自然対数を求め、そして、その結果の列の逆フーリエ変換を得ることにより計算されます [2]。
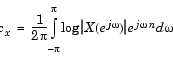
ツールボックスの関数rcepsは、この演算を行って列xの実数ケプストラムを出力します。出力される列は、入力ベクトルと同じ長さの実数値ベクトルです。
y = rceps(x)
定義に従って、実数ケプストラム変換からオリジナルの列を復元することはできません。それは、実数ケプストラムがデータ列のフーリエ変換の大きさのみに基づいているためです([2]を参照)。ただし、関数rcepsは、ケプストラム領域でウィンドウ関数を適用することにより、オリジナルのデータ列の最小位相形を復元することができます。データ列の実数ケプストラムと最小位相復元を共に得るには、つぎのようにします。
[y,ym] = rceps(x)
 | リサンプリング | 逆複素ケプストラム |  |