| 計算の信頼性 | |
スケーリング
特に、高次モデルの場合、状態空間は、LTIシステムにとって好ましいモデルです。ただし、状態空間モデルでも、コンピュータの有限ワード長算術のため正確な結果は保証されません。条件数の良い問題は、通常、正確な結果を得るための前提条件です。
条件数を改善するには、システム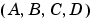
の行列を一般に正規化するか、スケーリングします。スケーリングが不適切な問題の例として、状態ベクトルの中に光年単位とミリメータ単位の状態量をもつダイナミックシステムを考えます。
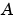行列は、非常に大きな数と非常に小さな数の両方を含むことが予想されます。数値が広い範囲に渡る行列は、逆行列と固有値問題のいずれの面でも条件数が悪い場合が多くあり、結果は不正確になります。
正規化は、さまざまな入力、出力の可制御性、可観測性の程度についても意味のあるステートメントを可能にします。
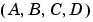行列の集合は、u、x、yをスケーリングする対角スケーリング行列
、
、
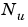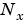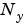を用いて正規化することができます。
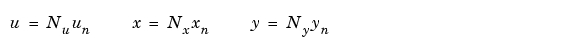
適切な正規化手順に従って、対角スケーリング行列を選択します。1つの基準は、入力、状態、出力変数のそれぞれの最大範囲を選択することです。この方法は、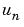
、 
、
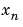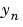が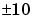
ボルトの範囲に設定を強いられたアナログシミュレーションコンピュータの時代に始まりました。第2の方法は、対角入力が各変数にとって重要な最小の誤差であるスケーリング行列を作成することです。LINPACK Users' Guide, [1]の導入部分には、スケーリングに関する優れた説明が記載されています。
スケーリングは、実際の問題に対する洞察に基づいて選択してください。スケーリングを行わないことにし、また多くの小さな問題に対して、スケーリングが不必要な場合には、この選択によって解の精度が影響されることに注意してください。
最後に、関数ssbalは、状態ベクトルの自動スケーリングを実行することに注意してください。特に、ssbalは、対角スケーリング行列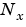
を用いることによって、つぎの行列のノルムを最小化しようとします。
そのような対角スケーリングは、数値範囲を圧縮し、それ以降の状態空間計算の条件数を改善するための経済的な方法です。
| | 零点-極-ゲインモデル | まとめ | |
