計算の信頼性

数値的安定性

数値的安定性について、納得がいくように説明することは困難です。詳細については、[5]、[6]、[7]の参考文献を参照してください。ここでは、安定性と条件数の違いを説明する簡単な例題を示します。

線形システム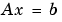 の解を求めるためのピボットの選択を伴わないGauss消去法は、数値的に不安定であることが知られています。つぎの行列を考えます。

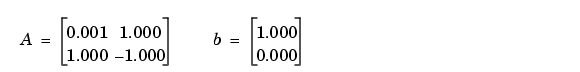
すべての計算は、3桁の有効数字による10進演算で行います。真の解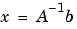は、近似的につぎのようになります。

第1行をピボット行として用いて(すなわち、第2行から第1行を1000倍して、減算する)、つぎのような等価の三角システムを得ます。

第2方程式の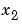に乗算される係数は、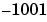ですが、丸めのために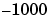となります。その結果、第2方程式は、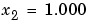となり、良好な近似となりますが、ここで第1方程式の後退代入、

の結果は、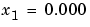となります。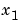のこのきわめて不適切な近似は、数値的不安定さの結果です。問題自体は、きわめて適切な条件数のように表示される可能性があります。勿論、MATLABでは、ピボット選択を伴うGauss消去法を実現しています。

条件数

LTIモデルの選択