計算の信頼性

条件数

つぎの線形システムについて考えます。

A =
    0.7800    0.5630
    0.9130    0.6590
b =
    0.2170
    0.2540

真の解は、x = [1, -1]'で、これは、MATLABを用いて、近似的に計算することができます。

x = A\b
x =
     1.0000
    -1.0000

format long, x
x =
     0.99999999991008
    -0.99999999987542

もちろん、実際の問題では真の解を知ることは、ほとんどありません。この問題は、条件数がきわめて悪いものです。それを確認するために、Aに対して、小さな摂動を付加します。

E =
     0.0010     0.0010
    -0.0020    -0.0010

ついで、摂動システムを解きます。

xe = (A+E)\b
xe =
    -5.0000
     7.3085

データ上の小さな変化が、解において、どれほど増大されるかという点に注意してください。

どれほど増幅されるかを測定する方法のひとつは、逆行列を使って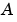の条件数と呼ばれる

を計算する方法です。条件数は、Gauss消去法での丸め誤差による精度損失を決定し、逆行列および線形方程式の解から得られる結果の精度を推定するために使用することができます。それは、摂動の影響を受けた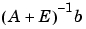解 を真の解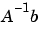と比較する摂動理論で自然に発生します。

MATLABでは、関数condが、2つのノルムの条件数を計算します。cond(A)は、Aの最大特異値と最小特異値との比です。それを上記の例題で試してみてください。通常のルールでは、条件数上の指数log10(cond(A))が、丸め誤差としてコンピュータが失う可能性のある小数点の数を示します。

IEEE規格の倍精度の数値は、精度が約16桁の10進数です。従って、行列が10¹⁰の条件数をもっている場合、解のうちの6桁だけが正確であると期待できます。条件数が、 1/sqrt(eps)よりはるかに大きい場合、それ以降の計算には注意が必要です。IEEE算術の場合、マシンの精度epsは、約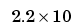^-16で、従って、1/sqrt(eps) = 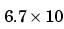⁸になります。

条件数に関して、もう1つ重要な側面は、一般に問題の条件数が良好な場合にのみ残差が精度の信頼できる指標となるということです。例証として、2つの解の候補x = [0.999 -1.001]'とx = [0.341 -0.087]'に対する残差ベクトル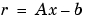を計算してみます。明らかに、かなり低い精度の解ですが、第2の解が、はるかに小さな残差を生成します。結論は、条件数の悪い問題にとって、残差は相対的な解の精度指標としては信頼性が低いということです。これは、問題の条件を正確に計算したり、推定したりする際に注意すべき最もな理由です。

条件数の悪い問題のもう1つの簡単な例題は、最初の上位対角に1をもつ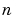行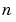列の行列です。

A = diag(ones(1,n-1),1);

この行列は、0に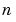個の固有値をもっています。ここで、数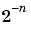をAの最終(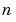番目の)行の第1要素に追加してできるデータの小さな摂動について考えてみます。この摂動行列は、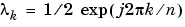を伴う異なるn 個の固有値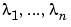をもっています。このように、データの小さな摂動は、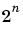の倍率で拡大され、解(Aの固有値)では大きな摂動となることがわかります。詳細と関連する例題については、参考文献[7]を参照してください。

逆行列に関して、行列の条件数が悪い場合も良い固有問題をもつ場合があり、また、その逆の場合もあることを理解する必要があります。たとえば、1の上三角行列(対角の下がゼロ)について考えてみます。

A = triu(ones(n));

この行列は、その固有問題(たとえば、n=20であるA(n,1)の小さな摂動を試みます)に関しては、条件数が悪い設定ですが、逆行列(その条件数を確認します)に関しては、良い条件数になっています。一方、行列

は、条件数が良い固有問題ですが、小さな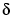に対する逆行列に関しては、悪い条件数となっています。

条件数および数値的安定性

数値的安定性