LTI Models (モデルの作成と取り扱い)

モデルの作成と取り扱い

周波数応答データ(FRD)モデル

時として、解析したり、制御したりするシステムに対して、伝達関数または状態空間モデルでなくサンプリングされた周波数応答データをもっている場合があります。線形システムの周波数応答解析の情報については、参考文献[1]の8章を参照してください。

たとえば、モデル化するSISOシステムに対する周波数応答関数をG(w)とします。そして、設定した周波数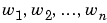でのG(w)を得る実験を行います。これは、つぎに示すように、対応する周波数をもった正弦波をシステムに入力することにより、実現します。

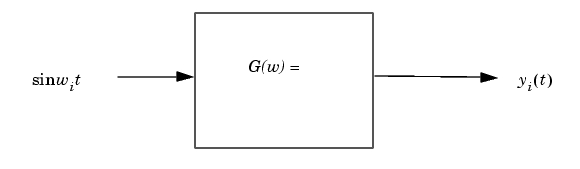
ここで、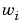は、i = 1 ... nでG(w) = 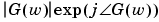の各正弦波の入力周波数です。このシステムの定常状態出力応答は、

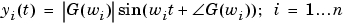
を満足します。周波数応答データ(FRD)オブジェクトは、シミュレーションや実験により得た周波数応答データ(設定した周波数点から構成されるベクトルとそれに対応する複素周波数応答)をストアして使うことができるモデルです。この例題で、周波数応答データは、周波数と応答の組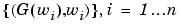から構成されます。

データをFRDモデルでストアすると、それをLTIモデルとして取り扱うことができ、TF,SS,ZPKと同様な取り扱いをすることができます。

SISO FRDモデル作成の基本的な構文は、つぎの型をしています。

sys = frd(response,frequencies,units)

ここで、

frequenciesは、長さNfの実数ベクトル

responseは、周波数に対する複素周波数応答値で長さNfのベクトル

unitsは、周波数単位を設定するオプションの文字列です。'rad/s'(デフォルト)または'Hz'を使用できます。

たとえば、MATファイルLTIexamples.matは、周波数ベクトルfreq、対応する複素周波数応答データベクトルrespGを含んでいます。この周波数領域データをロードして、FRDモデルを作成するため、つぎのように入力します。

load LTIexamples
sys = frd(respG,freq)
Continuous-time frequency response with 1 output and 1 input
at 5 frequency points.
From input 1 to: 
Frequency(rad/s)        output 1     
----------------        --------     
        1         -0.812505 -0.000312i
        2         -0.092593 -0.462963i
        4         -0.075781 -0.001625i
        5         -0.043735 -0.000390i

MIMO FRDモデルを作成する構文は、responseがp- m - Nfの多次元配列であることを除いて、SISOの場合と同じです。ここで、pは出力数、mは入力数、Nfは周波数データ点数(frequencyの長さ)です。

つぎの表は、FRDモデルに対する複素数値応答データフォーマットをまとめたものです。

表 1-3: FRDモデルで使う引数に対応するデータフォーマット
モデル形式

応答データフォーマット

SISOモデル

response(i) が周波数frequency(i)での周波数応答である長さNfのベクトル

MIMOモデル(出力数Ny、入力数Nu)

Ny - Nu - Nfの多次元配列をもち、response(i,j,k)は、周波数frequency(k)での入力jから出力iまでの周波数応答

S1 - S2 - .... -Sn配列のモデル(出力数Ny、入力数Nu)

Ny - Nu - S1 - ... - Snの多次元配列をもち、response(i,j,k,:)は、周波数frequency(k)で入力jから出力iまでの周波数応答データの配列です。

**表 1-3: FRDモデルで使う引数に対応するデータフォーマット**
モデル形式		応答データフォーマット
SISOモデル		`response(i)` が周波数`frequency(i)`での周波数応答である長さ`Nf`のベクトル
MIMOモデル(出力数`Ny`、入力数`Nu`)		`Ny` - `Nu` - `Nf`の多次元配列をもち、`response(i,j,k)`は、周波数`frequency(k)`での入力`j`から出力`i`までの周波数応答
`S1` - `S2` - .... -`Sn`配列のモデル(出力数`Ny`、入力数`Nu`)		`Ny` - `Nu` - `S1` - ... - `Sn`の多次元配列をもち、`response(i,j,k,:)`は、周波数`frequency(k)`で入力`j`から出力`i`までの周波数応答データの配列です。

ディスクリプタ状態空間モデル離散時間モデル