設計ケーススタディ

時変設計

Control System Toolboxは、時変Kalmanフィルタ処理を実行するための特定のコマンドは提供しませんが、MATLABでリカーシブフィルタを実行するのは容易です。この節では、上で検討した定常プラントに対して、これを実行する方法について説明します。

まず、ノイズの加わった観測量を生成します。

% 上で生成したプロセスノイズwと観測ノイズvを使用
sys = ss(A,B,C,0,-1);
y = lsim(sys,u+w);     % w = プロセスノイズ
yv = + v;            % v = 観測ノイズ

つぎの初期条件が与えられた場合、

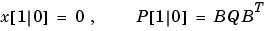
つぎのforループをもつ時変フィルタを実行することができます。

P = B*Q*B';         % 初期誤差共分散
x = zeros(3,1);     % 状態に対する初期条件
ye = zeros(length(t),1);
ycov = zeros(length(t),1); 

for i=1:length(t)
  % 観測値の更新
  Mn = P*C'/(C*P*C'+R);
  x = x + Mn*(yv(i)-C*x);   % x[n|n]
  P = (eye(3)-Mn*C)*P;      % P[n|n]

  ye(i) = C*x;
  errcov(i) = C*P*C';

  % 時刻の更新
  x = A*x + B*u(i);        % x[n+1|n]
  P = A*P*A' + B*Q*B';     % P[n+1|n]
end

ここで、真の出力と推定出力をグラフ上で比較することができます。

subplot(211), plot(t,y,'--',t,ye,'-') 
subplot(212), plot(t,y-yv,'-.',t,y-ye,'-')

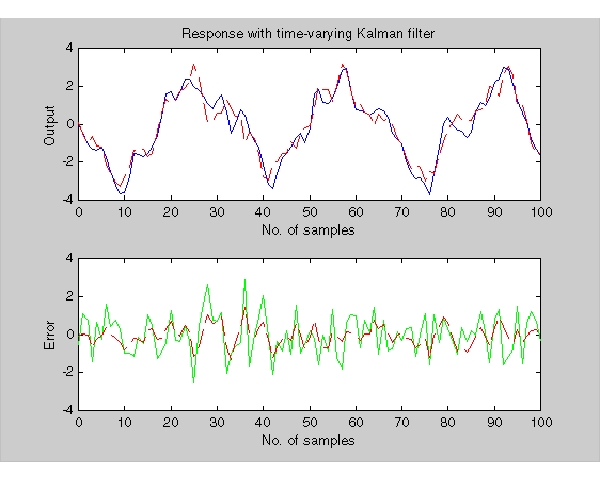
最初のプロットは、真の応答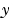(破線)とフィルタを適用した応答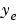(実線)を示しています。第2のプロットは、測定誤差(鎖線と点)と推定誤差(実線)を比較しています。

時変フィルタは、サンプルごとの推定誤差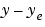の共分散errcovも推定します。それをプロットして、フィルタが(定常入力ノイズで期待されるとおりに)定常状態に達したかどうかを確認します。

subplot(211)
plot(t,errcov), ylabel('Error covar')

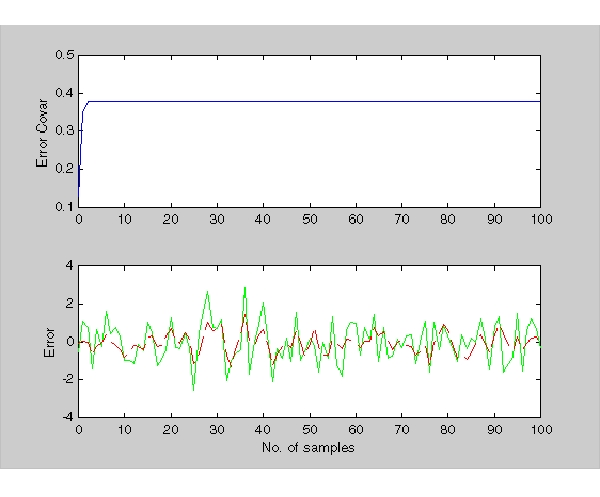
この共分散プロットから、出力共分散がおよそ5つのサンプルで実際に定常状態に達したことを確認できます。それ以降、時変フィルタは定常状態バージョンと同じ性能を維持します。

実験データから導いた推定誤差共分散と比較します。

EstErr = y-ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov =
    0.2718

この値は、理論値errcovより小さく、定常状態設計に対して得られる値に近くなります。

最後に、最終値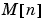とイノベーションゲイン行列の定常状態値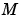が、つぎのように一致することに注意してください。

Mn, M

Mn =
    0.3798
    0.0817
   -0.2570

M =
    0.3798
    0.0817
   -0.2570

時変Kalmanフィルタ

参考文献