MATLAB Function Reference

ellipke

第1種と第2種の完全楕円積分

表示

K = ellipke(M)
[K,E] = ellipke(M)
[K,E] = ellipke(M,tol)

定義

第1種完全楕円積分(参考文献[1])は、次式で定義されます。

ここで、第1種楕円積分F は次式に対応します。

第2種完全楕円積分

は、次式で定義されます。

K とE の定義によっては、パラメータ m の代わりに母数k を使うことがあります。次式のような関係があります。

詳細

K = ellipke(M) は、M の要素に対して第１種完全楕円積分を出力します。

[K,E] = ellipke(M) は、第1種および第2種の完全楕円積分を出力します。

[K,E] = ellipke(M,tol) は、精度 tolでヤコビアン楕円関数を計算します。デフォルトは epsで、この値を大きくすると、計算精度は低くなりますが、より高速に計算が行われます。

アルゴリズム

ellipke は、参考文献[1] の 17.6節に記載されている算術幾何平均を使って完全楕円積分を計算します。つぎの3つの値からはじめます。

ellipke は、次式を使って a_i, b_i, c_iの逐次代入を行います。

これは、epsで指定される許容値内で、cn 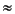0 となるとき、n の繰り返し回数で停止します。このとき、第1種完全楕円積分は、つぎのようになります。

制限

関数ellipke への入力定義域は、に制限されます。

参考

ellipj

参考文献

[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.

ellipj

else