ellipj (MATLAB Function 参考文献)

ヤコビアン楕円関数

表示

[SN,CN,DN]  =  ellipj(U,M)
[SN,CN,DN]  =  ellipj(U,M,tol)

定義

ヤコビアン楕円関数は、つぎの積分項で定義されます。

このとき、

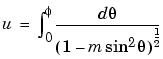
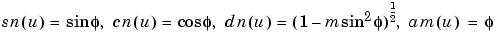
です。楕円関数の定義によっては、パラメータ m の代わりに母数 k を使うことがあります。次式のような関係があります。

:

ヤコビアン楕円関数は多くの数学的な認識に従っています。良い例として、参考文献[1]を参照してください。

詳細

[SN,CN,DN] = ellipj(U,M) は、対応する U と M の要素に対して評価される、ヤコビアン楕円関数 SN, CN, DN を出力します。入力 U, M は、同じサイズ(あるいは、どちらかがスカラ)でなければなりません。

[SN,CN,DN] = ellipj(U,M,tol) は、精度 tol でヤコビアン楕円関数を計算します。デフォルトは、eps で、この値を大きくすると、計算精度は低くなりますが、より高速に計算が行われます。

アルゴリズム

ellipjは、算術幾何平均(参考文献[1])を使ってヤコビアン楕円関数を計算します。つぎの3つの値からはじめます。

ellipj は、次式を使って逐次代入法を行います。

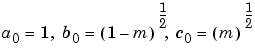
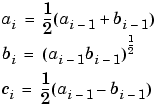
つぎに、位相の連続性に注意して、次式からラジアン単位で振幅を計算します。

このとき、ヤコビアン楕円関数は簡単に次式で表されます。

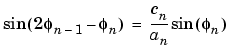
制限

関数ellipj への入力定義域は、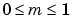に制限されます。参考文献[1] に記載されている変換式 16.10 と 16.11を使って、この範囲に M の他の値を写像します。Uは実数値に制限されます。

参考

参考文献

[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.

eigs ellipke