

| MATLAB Function Reference |   |
表示
H = besselh(nu,K,Z) H = besselh(nu,Z) H = besselh(nu,1,Z,1) H = besselh(nu,2,Z,1) [H,ierr] = besselh(...)
定義
は、Bessel 方程式と云われ、その解は、Bessel関数として知られているものです。ここで、 は、非負の定数です。
整数でない
は、非負の定数です。
整数でない に対して、Bessel方程式の解の基本部分を構成するものは、
に対して、Bessel方程式の解の基本部分を構成するものは、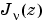 と
と 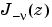 です。
です。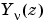 は、
は、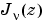 に線形独立な Bessel 方程式の2番目の解で、つぎの関係を示します。
に線形独立な Bessel 方程式の2番目の解で、つぎの関係を示します。

Hankel 関数と Bessel 関数の関係は、つぎのようになります。

詳細
H = besselh(nu,K,Z)
は、K = 1 、または、2 に従って、Hankel関数
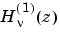 、または、
、または、
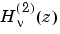 を、複素数配列
を、複素数配列Zの各要素に対して、計算します。nu と Z が、同じサイズの配列の場合、結果も同じサイズになります。どちらかの入力がスカラの場合は、展開して、他の入力の大きさになります。一つの入力が行ベクトルで、他が列ベクトルの場合、結果は、関数値からなる2次元のテーブルになります。
H = besselh(nu,Z)
は、K = 1を使います。
H = besselh(nu,1,Z,1)
は、 を
を exp(-i*z)でスケーリングします。
H = besselh(nu,2,Z,1)
は、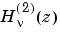 を
を exp(+i*z)でスケーリングします。
[H,ierr] = besselh(...)
は、エラーフラッグの配列も出力します。
ierr = 1 |
|
ierr = 2 |
|
ierr = 3 |
|
ierr = 4 |
|
ierr = 5 |
 | beep | besseli, besselk |  |