Mathematics

多変数回帰

yが複数の独立変数からなる関数ならば、変数間の関係を表す行列方程式は、追加データを集めて展開します。

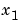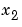パラメータ とのいくつかの値に対して、値 yを観測していると仮定しましょう。観測値を、つぎのように表すとします。

x1 = [.2 .5 .6 .8 1.0 1.1]';
x2 = [.1 .3 .4 .9 1.1 1.4]';
y  = [.17 .26 .28 .23 .27 .24]';

データの多変数モデルを、つぎのように考えます。

未知係数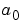,,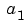 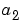に関して、多変数の解は、最小二乗近似を使って解きます。回帰行列Xを作成して連立方程式を作成し、バックスラッシュ演算子を使って係数を解きます。

X = [ones(size(x1))  x1  x2];
a = X\y

a =
    0.1018
    0.4844
   -0.2847

データの最小二乗モデルは、つぎのようになります。

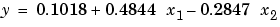
モデルを検証するために、モデルから求めた点と観測データ点の偏差の絶対値の最大値を求めます。

Y = X*a;
MaxErr = max(abs(Y - y))

MaxErr = 
     0.0038

この値は、データへの適合がうまくいっているモデルであることを確信できるほど十分に小さいものです。

パラメータが線形である方程式の回帰

ケーススタディ：カーブフィッテング