Mathematics

はじめに

長さNの入力列xに対して、DFTは長さNのベクトルXになります。fftとifftの関係は、つぎのようになります。

注意    MATLABベクトルの最初の要素は、インデックスが1としているので、上の方程式の和は、1からNまでのに対応し、通常、記述するフーリエの0からN-1までの和を使うものに対応します。

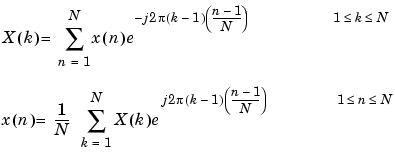
x(n) が実数の場合、上の方程式は、実数係数とsinとcos関数の和として表わすことができます。

ここで、つぎの関係があります。

列ベクトルxのFFT は、

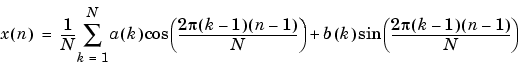
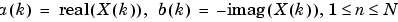
x = [4 3 7 -9 1 0 0 0]' ;

つぎのステートメントを使います。

y = fft(x)

結果は、つぎのようになります。

y =
6.0000
11.4853  -2.7574i
-2.0000 -12.0000i
-5.4853 +11.2426i
18.0000
-5.4853 -11.2426i
-2.0000 +12.0000i
11.4853 + 2.7574i

データ列xは実数で、yは複素数であることに注意してください。変換されたデータの最初の成分は、定数として機能し、5番目の要素はNyquist周波数に対応します。yの最後3つの値は、負の周波数に対応し、実数列xに対して、yの前半の3つの要素の複素共役になります。

この300年間の太陽の黒点の活動の変化を解析しましょう。太陽の黒点の活動は、約11年の周期をもっていることが知られています。確認して見ましょう。

天文学者は、ほぼ300年間のWolfer数と呼ばれる量の一覧をもっています。この中には、太陽の黒点の数と大きさを含んでいます。

太陽の黒点データをロードし、プロットします。

load sunspot.dat
year = sunspot(:,1);
wolfer = sunspot(:,2);
plot(year,wolfer)
title('Sunspot Data')

太陽の黒点データのFFTを計算します。

Y = fft(wolfer);

この変換の結果は、複素数ベクトルYになります。Yの二乗の大きさは、パワーとよばれ、周波数に対してパワーのプロットは、"ピリオドグラム"と言われます。すべてのデータを加算したYの最初の要素を取り除き、結果をプロットします。

N = length(Y);
Y(1) = [];
power = abs(Y(1:N/2)).^2;
nyquist = 1/2;
freq = (1:N/2)/(N/2)*nyquist;
plot(freq,power), grid on
xlabel('cycles/year')
title('Periodogram')

年数に関する周期性のスケーリングは、幾分不便なものです。何が1サイクルなのかを推定するため1サイクルに対する年数をプロットします。便宜的に、0から40years/cycleの周期に対してパワーをプロットします(周期はperiod = 1./freq)です)。

period = 1./freq;
plot(period,power), axis([0 40 0 2e7]), grid on
ylabel('Power')
xlabel('Period(Years/Cycle)')

周期性をより詳しく決めるために、

[mp index] = max(power);
period(index)

ans = 
      11.0769

関数のまとめ

変換されたデータのゲインと位相