Mathematics

過多システム

連立線形方程式の過多システムは、実験データの種々の曲線近似で使われています。ここでは、仮説の例題を考えましょう。値yは、時刻tで測定された観測値です。

t	y
0.0	0.82
0.3	0.72
0.8	0.63
1.1	0.60
1.6	0.55
2.3	0.50

このデータは、MATLABに、つぎのステートメントで読み込むことができます。

t = [0 .3 .8 1.1 1.6 2.3]';
y = [.82 .72 .63 .60 .55 .50]';

データは、指数的に減衰する関数でモデル化できるとします。

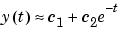
この方程式は、ベクトルyが、定数1を含む定数ベクトルと成分e^-tをもつベクトルの2つのベクトルの線形結合で近似するものです。未知係数c₁ とc₂は、モデルとデータとの偏差の二乗和を最小にする最小二乗を行なうことで計算します。ここでは、2つの未知数をもつ6つの方程式により、6行2列の行列で表されます。

E = [ones(size(t)) exp(-t)]

E =
      1.0000    1.0000
      1.0000    0.7408
      1.0000    0.4493
      1.0000    0.3329
      1.0000    0.2019
      1.0000    0.1003

最小二乗解は、バックスラッシュ演算で求まります。

c = E\y

c =
      0.4760
      0.3413      

別な表現をすると、データの最小二乗適合は、つぎのように表せます。

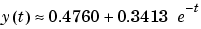
つぎのステートメントは、定間隔に刻まれた時刻tについて、モデルを計算し、オリジナルのデータと共にプロットします。

T = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T)]*c;
plot(T,Y,'-',t,y,'o')

E*cは、yと正確に一致はしません。が、その違いは、オリジナルデータの中に含まれる測定誤差よりもかなり小さいものです。

長方形行列Aは、線形に独立でない列があると、ランク落ちになります。Aがランク落ちならば、AX = Bの最小二乗解はユニークでなくなります。バックスラッシュ演算A\Bは、Aがランク落ちの状態なら、ワーニングを表示し、ゼロでない要素ができるだけ少ない基本解を出力します。

正方システム

過少システム