Mathematics

概要

技術計算の中で最も重要な問題の一つは、連立線形方程式を解くことです。行列記法の中で、この問題は、つぎのように記述できます。

2つの行列AとBを与え、つぎの2つの条件のいずれかを満足するユニークな行列Xが存在しますか?

1行1列の簡単な例を考えましょう。

つぎの方程式

は、ユニークな解をもっていますか？

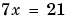
この解は、もちろん、'はい'です。方程式は、ユニークな解x = 3をもちます。方程式は割り算により簡単に解を得ます。

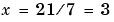
解は、通常、7の逆数、すなわち、7^-1 = 0.142857...を計算し、それを乗算する方法は、使いません。それで、7^-1に21を乗算します。仮に7^-1が有限の小数値で与えられば、精度は落ちますが、うまく機能します。複数の未知数をもった連立方程式に同様な考えを適用します。

標準の数学的な記法ではありませんが、MATLAB は、一般的な連立方程式を解く方法を記述するスカラの場合に良く使用する除算の方法を使います。2つの除算記号、スラッシュ/とバックラッシュ\が、未知の行列を係数行列の左除算、右除算を示します。

X = A\B	は、行列方程式AX = Bの解です。
X = B/A	は、行列方程式XA = Bの解です。

AX = BまたはXA = Bの方程式の両側をAで割ることを考えてください。係数行列Aは、常に分母になります。

X = A\Bに対する次元の整合性の条件は、2つの行列AとBが、同じ長さの行であることです。それで、解Xは、Bと同じ列数になり、行の大きさはAの列の大きさと等しくなります。X = B/Aにおいて、行と列の役割は、反転します。

実際に、AX = Bの線形方程式は、XA = Bの型のものよりも、非常に頻繁に生じます。結果として、バックスラッシュは、スラッシュよりも頻繁に使われます。この節の残りの部分は、バックスラッシュ演算を集中的に取り扱います。スラッシュ演算子の対応する性質は、つぎの等式から推定できます。

(B/A)' = (A'\B')

係数行列Aは、正方である必要がありません。Aがm行n列の行列ならば、つぎの3ケースが考えられます。

m = n	正方システム、厳密解が得られます。
m > n	過多システムで、最小二乗解を求めましょう。
m < n	過少システムで、m個のゼロでない成分をもつ基本解を求めます。

バックスラッシュ演算子は、種々のタイプの係数行列を取り扱うため、種々のアルゴリズムを使います。種々のケースで、係数行列を調べることにより、自動的に判断します。

• 三角行列の置換
• 対称、正定行列
• 正方、非特異行列
• 長方形、過多システム
• 長方形、過少システム

線形方程式の解法

正方システム