Symbolic Math Toolbox

Single Differential Equation

The function dsolve computes symbolic solutions to ordinary differential equations. The equations are specified by symbolic expressions containing the letter D to denote differentiation. The symbols D2, D3, ... DN, correspond to the second, third, ..., Nth derivative, respectively. Thus, D2y is the Symbolic Math Toolbox equivalent of 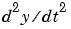. The dependent variables are those preceded by D and the default independent variable is t. Note that names of symbolic variables should not contain D. The independent variable can be changed from t to some other symbolic variable by including that variable as the last input argument.

Initial conditions can be specified by additional equations. If initial conditions are not specified, the solutions contain constants of integration, C1, C2, etc.

The output from dsolve parallels the output from solve. That is, you can call dsolve with the number of output variables equal to the number of dependent variables or place the output in a structure whose fields contain the solutions of the differential equations.

Example 1

The following call to dsolve

• dsolve('Dy=1+y^2')
  

uses y as the dependent variable and t as the default independent variable. The output of this command is

• ans = 
  tan(t+C1)
  

To specify an initial condition, use

• y = dsolve('Dy=1+y^2','y(0)=1')
  

This produces

• y =
  tan(t+1/4*pi)
  

Notice that y is in the MATLAB workspace, but the independent variable t is not. Thus, the command diff(y,t) returns an error. To place t in the workspace, type syms t.

Example 2

Nonlinear equations may have multiple solutions, even when initial conditions are given:

• x = dsolve('(Dx)^2+x^2=1','x(0)=0')
  

results in

• x =
  [-sin(t)]
  [ sin(t)]
  

Example 3

Here is a second order differential equation with two initial conditions. The commands

• y = dsolve('D2y=cos(2*x)-y','y(0)=1','Dy(0)=0', 'x')
  simplify(y)
  

produce

• y =
  -2/3*cos(x)^2+1/3+4/3*cos(x)
  

The key issues in this example are the order of the equation and the initial conditions. To solve the ordinary differential equation

simply type

• u = dsolve('D3u=u','u(0)=1','Du(0)=-1','D2u(0) = pi','x')
  

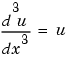
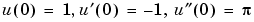
Use D3u to represent 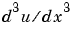and D2u(0) for .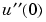

Several Algebraic Equations

Several Differential Equations