Using the Symbolic Math Toolbox (Symbolic Math Toolbox)

Symbolic Math Toolbox

Several Algebraic Equations

Now let's look at systems of equations. Suppose we have the system

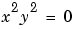
and we want to solve for x and y. First create the necessary symbolic objects.

```
syms x y alpha
```

There are several ways to address the output of solve. One is to use a two-output call

```
[x,y] = solve(x^2*y^2, x-y/2-alpha)
```

which returns

x = 
[     0]
[     0]
[ alpha]
[ alpha]

y = 
[ -2*alpha]
[ -2*alpha]
[        0]
[        0]

Consequently, the solution vector

```
v = [x, y]
```

appears to have redundant components. This is due to the first equation , which has two solutions in x and y: , . Changing the equations to

eqs1 = 'x^2*y^2=1, x-y/2-alpha'
[x,y] = solve(eqs1)

produces four distinct solutions:

x =
[ 1/2*alpha+1/2*(alpha^2+2)^(1/2)]
[ 1/2*alpha-1/2*(alpha^2+2)^(1/2)]
[ 1/2*alpha+1/2*(alpha^2-2)^(1/2)]
[ 1/2*alpha-1/2*(alpha^2-2)^(1/2)]
 
 
y =
[ -alpha+(alpha^2+2)^(1/2)]
[ -alpha-(alpha^2+2)^(1/2)]
[ -alpha+(alpha^2-2)^(1/2)]
[ -alpha-(alpha^2-2)^(1/2)]

Since we did not specify the dependent variables, solve uses findsym to determine the variables.

This way of assigning output from solve is quite successful for "small" systems. Plainly, if we had, say, a 10-by-10 system of equations, typing

[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10] = solve(...)

is both awkward and time consuming. To circumvent this difficulty, solve can return a structure whose fields are the solutions. In particular, consider the system u^2-v^2 = a^2, u + v = 1, a^2-2*a = 3. The command

S = solve('u^2-v^2 = a^2','u + v = 1','a^2-2*a = 3')

returns

S = 
    a: [2x1 sym]
    u: [2x1 sym]
    v: [2x1 sym]

The solutions for a reside in the "a-field" of S. That is,

```
S.a
```

produces

```
ans =
[ -1]
[  3]
```

Similar comments apply to the solutions for u and v. The structure S can now be manipulated by field and index to access a particular portion of the solution. For example, if we want to examine the second solution, we can use the following statement

```
s2 = [S.a(2), S.u(2), S.v(2)]
```

to extract the second component of each field.

```
s2 =
[  3,  5, -4]
```

The following statement

```
M = [S.a, S.u, S.v]
```

creates the solution matrix M

```
M = 
[ -1,  1,  0]
[  3,  5, -4]
```

whose rows comprise the distinct solutions of the system.

Linear systems of simultaneous equations can also be solved using matrix division. For example,

clear u v x y
syms u v x y
S = solve(x+2*y-u, 4*x+5*y-v);
sol = [S.x;S.y]

and

```
A = [1 2; 4 5];
b = [u; v];
z = A\b
```

result in

sol =
 
[ -5/3*u+2/3*v]
[  4/3*u-1/3*v]

z =
[ -5/3*u+2/3*v]
[  4/3*u-1/3*v]

Thus s and z produce the same solution, although the results are assigned to different variables.

Solving Equations Single Differential Equation