Symbolic Math Toolbox

Singular Value Decomposition

Only the variable-precision numeric computation of the complete singular vector decomposition is available in the toolbox. One reason for this is that the formulas that result from symbolic computation are usually too long and complicated to be of much use. If A is a symbolic matrix of floating-point or variable-precision numbers, then

• S = svd(A)
  

computes the singular values of A to an accuracy determined by the current setting of digits. And

• [U,S,V] = svd(A);
  

produces two orthogonal matrices, U and V, and a diagonal matrix, S, so that

• A = U*S*V';
  

Let's look at the n-by-n matrix A with elements defined by

• A(i,j) = 1/(i-j+1/2)
  

For n = 5, the matrix is

• [  2    -2   -2/3   -2/5   -2/7]
  [2/3     2     -2   -2/3   -2/5]
  [2/5   2/3      2     -2   -2/3]
  [2/7   2/5    2/3      2     -2]
  [2/9   2/7    2/5    2/3      2]
  

It turns out many of the singular values of these matrices are close to .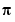

The most obvious way of generating this matrix is

• for i=1:n
      for j=1:n
        A(i,j) = sym(1/(i-j+1/2));
     end
  end
  

The most efficient way to generate the matrix is

• [J,I] = meshgrid(1:n);
  A = sym(1./(I - J+1/2));
  

Since the elements of A are the ratios of small integers, vpa(A) produces a variable-precision representation, which is accurate to digits precision. Hence

• S = svd(vpa(A))
  

computes the desired singular values to full accuracy. With n = 16 and digits(30), the result is

• S = 
  [ 1.20968137605668985332455685357 ]
  [ 2.69162158686066606774782763594 ]
  [ 3.07790297231119748658424727354 ]
  [ 3.13504054399744654843898901261 ]
  [ 3.14106044663470063805218371924 ]
  [ 3.14155754359918083691050658260 ]
  [ 3.14159075458605848728982577119 ]
  [ 3.14159256925492306470284863102 ]
  [ 3.14159265052654880815569479613 ]
  [ 3.14159265349961053143856838564 ]
  [ 3.14159265358767361712392612384 ]
  [ 3.14159265358975439206849907220 ]
  [ 3.14159265358979270342635559051 ]
  [ 3.14159265358979323325290142781 ]
  [ 3.14159265358979323843066846712 ]
  [ 3.14159265358979323846255035974 ]
  

There are two ways to compare S with pi, the floating-point representation of 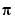. In the vector below, the first element is computed by subtraction with variable-precision arithmetic and then converted to a double. The second element is computed with floating-point arithmetic:

• format short e
  [double(pi*ones(16,1)-S)  pi-double(S)]  
  

The results are

•    1.9319e+00   1.9319e+00
     4.4997e-01   4.4997e-01
     6.3690e-02   6.3690e-02
     6.5521e-03   6.5521e-03
     5.3221e-04   5.3221e-04
     3.5110e-05   3.5110e-05
     1.8990e-06   1.8990e-06
     8.4335e-08   8.4335e-08
     3.0632e-09   3.0632e-09
     9.0183e-11   9.0183e-11
     2.1196e-12   2.1196e-12
     3.8846e-14   3.8636e-14
     5.3504e-16   4.4409e-16
     5.2097e-18            0
     3.1975e-20            0
     9.3024e-23            0
  

Since the relative accuracy of pi is pi*eps, which is 6.9757e-16, either column confirms our suspicion that four of the singular values of the 16-by-16 example equal 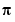to floating-point accuracy.

Jordan Canonical Form

Eigenvalue Trajectories