Spline Toolbox

Comparison and Extension

The second approach is more symmetric than the first in that transposition takes place in each call to spap2 and nowhere else. This approach can be used for approximation to gridded data in any number of variables.

If, for example, the given data over a three-dimensional grid are contained in some three-dimensional array v of size [Nx,Ny,Nz], with v(i,j,k) containing the value 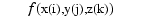, then we would start off with

• coefs = reshape(v,Nx,Ny*Nz);
  

Assuming that nj = knotsj - kj, for j = x,y,z, we would then proceed as follows: 

• sp = spap2(knotsx,kx,x,coefs.');
  coefs = reshape(fnbrk(sp,'c'),Ny,Nz*nx);
  sp = spap2(knotsy,ky,y,coefs.'); 
  coefs = reshape(fnbrk(sp,'c'),Nz,nx*ny);
  sp = spap2(knotsz,kz,z,coefs.'); 
  coefs = reshape(fnbrk(sp,'c'),nx,ny*nz);
  

See Chapter 17 of PGS or [C. de Boor, "Efficient computer manipulation of tensor products," ACM Trans. Math. Software 5 (1979), 173-182; Corrigenda, 525] for more details. The same references also make clear that there is nothing special here about using least squares approximation. Any approximation process, including spline interpolation, whose resulting approximation has coefficients that depend linearly on the given data, can be extended in the same way to a multivariate approximation process to gridded data. 

This is exactly what is used in the spline construction commands csapi, csape, spapi, spaps, and spap2, when gridded data are to be fitted. It is also used in fnval, when a tensor product spline is to be evaluated on a grid.

The Bivariate Approximation

Reference