Spline Toolbox

The Bivariate Approximation

The claim is that coefsb equals the earlier coefficient array coefs, up to round-off, and here is the test:

• disp( max(max(abs(coefs - coefsb))) ) 
  1.4433e-15
  

The explanation is simple enough: The coefficients c of the spline 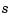contained in sp = spap2(knots,k,x,y) depend linearly on the input values 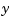. This implies, given that both c and y are 1-row matrices, that there is some matrix 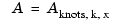so that

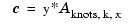
for any data y. This statement even holds when y is a matrix, of size 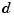-by-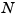, say, in which case each datum 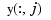is taken to be a point in 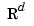, and the resulting spline is correspondingly 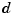-vector-valued, hence its coefficient array c is of size 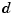-by-n, with n = length(knots)-k.

In particular, the statements

• sp = spap2(knotsy,ky,y,z); 
  coefsy =fnpbrk(sp,'c');
  

provide us with the matrix coefsy that satisfies

The subsequent computations

•  sp2 = spap2(knotsx,kx,xx,coefsy.'); 
   coefs = fnbrk(sp2,'c').';
  

generate the coefficient array coefs, which, taking into account the two transpositions, satisfies

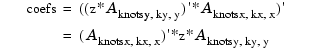
In the second, alternative, calculation, we first computed

•  spb = spap2(knotsx,kx,x,z.'); 
   coefsx = fnbrk(spb,'c');
  

hence

. The subsequent calculation

•  spb2 = spap2(knotsy,ky,y,coefsx.');
   coefsb = fnbrk(spb,'c');
  

then provided

Consequently, coefsb = coefs.

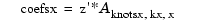
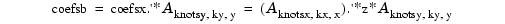
Approximation to Coefficients as Functions of y

Comparison and Extension