Spline Toolbox

Iteration

We can now complete the construction and solution of the linear system for the improved approximate solution z from our current guess y. In fact, with the initial guess y available, we now set up an iteration, to be terminated when the change 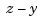is small enough. We choose a relatively mild .

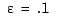• epsilon =.1;
  tolerance=1.e-9;
  while 1 
    vtau=fnval(y,colpnts); 
    weights = [0 1 0; 
              [2*vtau.'zeros(8,1) epsilon*ones(8,1)]; 
               1 0 0]; 
    colloc = zeros(10,10); 
    for j=1:10 
       colloc(j,:)=weights(j,:)*colmat(3*(j-1)+[1:3],:); 
    end 
    coefs = colloc\[0 vtau.*vtau+1 0].'; 
    z = spmak(knots,coefs.'); 
    maxdif = max(abs(z-y)) 
  if maxdif<tolerance, break, end 
      y = z; 
  end
  

The resulting printout of the errors

• maxdif = 0.2067 
  maxdif = 0.0121 
  maxdif = 3.9515e-005 
  maxdif = 4.4322e-010
  

shows the quadratic convergence expected from Newton's method. The plot below shows the initial guess and the computed solution, as the two leftmost curves. Note that the computed solution, like the exact solution, does not equal -1 at 0.

Figure 2-16: Solutions of a Nonlinear ODE with Increasingly Strong Boundary Layer

If we now decrease 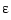, we create more of a boundary layer near the right endpoint, and this calls for a nonuniform mesh.

We use newknt to construct an appropriate finer mesh from the current approximation:

• knots = newknt(z, ninterv+1); breaks = knt2brk(knots);
  knots = augknt(breaks,4,2); 
  n = length(knots)-k;
  

From the new break sequence, we generate the new collocation site sequence:

• ninterv = length(breaks)-1; 
  temp = ((breaks(2:ninterv+1)+breaks(1:ninterv))/2); 
  temp = temp([1 1], :) + gauss*diff(breaks); 
  colpnts = temp(:).'; 
  sites = [0,colpnts,1];
  

We use spcol to supply the matrix

• colmat = spcol(knots,k,sort([sites sites sites]));
  

and use our current approximate solution z as the initial guess:

• intmat = colmat([2 1+[1:(n-2)]*3,1+(n-1)*3],:); 
  y = spmak(knots,[0 fnval(z,colpnts) 0]/intmat.');
  

Thus set up, we cut 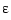by 3 and repeat the earlier calculation, starting with the statements

• tolerance=1.e-9; 
  while 1 
    vtau=fnval(y,colpnts);
    .
    .
    .
  

Repeated passes through this process generate a sequence of solutions, for 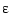 = 1/10, 1/30, 1/90, 1/270, 1/810. The resulting solutions, ever flatter at 0 and ever steeper at 1, are shown in the plot above. The plot also shows the final break sequence, as a sequence of vertical bars.

In this example, at least, newknt has performed satisfactorily.

Linear System to Be Solved

Example: Construction of the Chebyshev Spline