| Spline Toolbox | |
Linear System to Be Solved
Since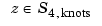 
, we convert this last system into a system for the B-spline coefficients of 
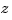. This requires the values, first, and second derivatives at every 
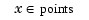and for all the relevant B-splines. The command spcol was expressly written for this purpose.
We use spcol to supply the matrix
From this, we get the collocation matrix by combining the row triple of colmat for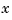 
using the weights 
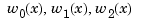to get the row for 
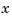of the actual matrix. For this, we need a current approximation 
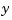. Initially, we get it by interpolating some reasonable initial guess from our piecewise-polynomial space at the sites. We use the parabola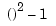 
(i.e., the function
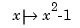) which satisfies the end conditions as the initial guess, and pick the matrix from the full matrix colmat. Here it is, in several cautious steps:
intmat = colmat([2 1+[1:8]*3,1+9*3],:); coefs = intmat\[0 colpnts.*colpnts-1 0].'; y = spmak(knots,coefs.');
| | Linearization | Iteration | |