| Spline Toolbox | |
Use
Having chosen to represent the rational spline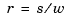 
in this way by the ordinary spline 
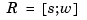makes it is easy to apply to a rational spline all the fn... commands in the Spline Toolbox, with the following exceptions. The integral of a rational spline need not be a rational spline, hence there is no way to extend fnint to rational splines. The derivative of a rational spline is again a rational spline but one of roughly twice the order. For that reason, fnder and fndir will not touch rational splines. Instead, there is the command fntlr for computing the value at a given x of all derivatives up to a given order of a given function. If that function is rational, the needed calculation is based on the considerations given in the preceding paragraph.
A special rational spline, called a NURBS, has become a standard tool in CAGD. A NURBS is, by definition, any rational spline for which both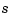 
and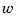 
are in B-form, with each coefficient for 
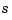containing explicitly the corresponding coefficient for 
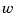as a factor:
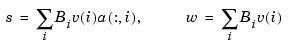
The normalized coefficients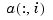 
for the numerator spline are more readily used as control points than the unnormalized coefficients 
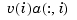. Nevertheless, this toolbox provides no special NURBS form, but only the more general rational spline, but in both B-form (called rBform internally) and in ppform (called rpform internally).
The rational spline circle used earlier is put together in rsmak by commands like the following.
x = [1 1 0 -1 -1 -1 0 1 1]; y = [0 1 1 1 0 -1 -1 -1 0]; s45 = 1/sqrt(2); w =[1 s45 1 s45 1 s45 1 s45 1]; circle = rsmak(augknt(0:4,3,2), [w.*x;w.*y;w]);
Note the appearance of the denominator spline as the last component. Also note how the coefficients of the denominator spline appear here explicitly as factors of the corresponding coefficients of the numerator spline. The normalized coefficient sequence [x;y] is very simple; it consists of the vertices and midpoints, in proper order, of the "unit square". The resulting control polygon is tangent to the circle at the places where the four quadratic pieces that form the circle abut.
For a thorough discussion of NURBS, see [G. Farin, NURBS, 2nd ed., AKPeters Ltd, 1999] or [Les Piegl and Wayne Tiller, The NURBS Book, 2nd ed., Springer-Verlag, 1997].
| | rsform | The stform | |