| Spline Toolbox | |
rsform
Offhand, the two splines,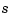 
and 
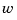, in the rational spline 
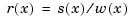need not be related to one another. They could even be of different forms. But, in the context of this toolbox, it is convenient to restrict them to be of the same form, and even of the same order and with the same breaks or knots. For, under that assumption, we can (and do) represent such a rational spline by the (vector-valued) spline function
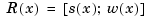
whose values are vectors with one more entry than the values of the rational spline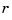 
. It is very easy to obtain 
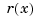from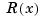 
. For example, if v is the value of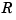 
at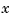 
, then v(1:end-1)/v(end) is the value of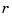 
at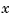 
. If, in addition, dv is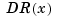 
, then (dv(1:end-1)-dv(end)*v(1:end-1))/v(end) is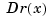 
. More generally, by Leibniz's formula,
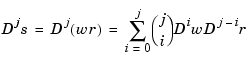
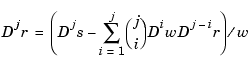
This shows that we can compute the derivatives of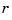 
inductively, using the derivatives of 
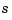and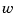 
(i.e., the derivatives of 
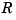) along with the derivatives of 
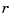of order less than 
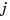to compute the 
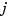th derivative of 
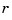. There is a corresponding formula for partial and directional derivatives for multivariate rational splines.
| | Example: Sphere | Use | |