| Spline Toolbox | |
Convert locally from B-form to ppform
Syntax
Description
These are utility commands of use in the conversion from B-form to ppform (and in certain evaluations), but of no interest to the casual user.
[v,b] = splpp(tx,a)
provides the matrices v and b, both of the same size [r,k] as a, and related to the input in the following way.
For i=1:r, b(i,:) are the B-coefficients, with respect to the knot sequence [tx(i,1:k-1),0,...,0], of the polynomial of order k on the interval [tx(i,k-1) .. tx(i,k)] whose k B-spline coefficients, with respect to the knot sequence tx(i,:), are in a(i,:). This is done by repeated knot insertion (of the knot 0). It is assumed that tx(i,k-1)<0<=tx(i,k).
For i=1:r, v(i,:) are the polynomial coefficients for that polynomial, i.e., v(i,j) is the number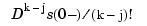 
, j=1:k, with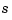 
having the knots tx(i,:) and the B-coefficients a(i,:).
[v,b] = sprpp(tx,a)
carries out exactly the same job, except that now b(i,:) are the B-coefficients for that polynomial with respect to the knot sequence [0,...,0,tx(i,k: 2*(k-1))], and, correspondingly, v(i,j) is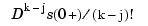 
, j=1:k. Also, now it is assumed that tx(i,k-1)<=0<tx(i,k).
Examples
The statement [v,b]=splpp([-2 -1 0 1],[0 1 0]) provides the sequence
with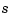 
the B-spline with knots -2, -1, 0, 1. This is so because the l in splpp indicates the limit from the left, and the second argument, [0 1 0], indicates the spline s in question to be
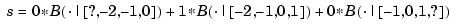
i.e., this particular linear combination of the third-order B-splines for the knot sequence ..., -2, -1,0,1,... (Note that the values calculated do not depend on the knots marked ?.) The above statement also provides the sequence b = 0 1.0000 0.5000 of B-spline coefficients for the polynomial piece of s on the interval [-1. .0], and with respect to the knot sequence ?, -2, -1, 0, 0, ?.
In other words, on the interval [-1. .0], the B-spline with knots 2, -1, 0, 1 can be written
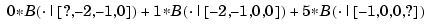
The statement [v,b]=sprpp([-1 0 1 2],[1 0 0]) provides the sequence
with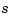 
the B-spline with knots ?,-1,0,1. Its polynomial piece on the interval [0..1] is independent of the choice of ?, so we might as well think of ? as -2, i.e., we are dealing with the same B-spline as before. Note that the last two numbers agree with the limits from the left computed above, while the first number does not. This reflects the fact that a quadratic B-spline with simple knots is continuous with continuous first, but discontinuous second, derivative. (It also reflects the fact that the left-most knot of a B-spline is irrelevant for its right-most polynomial piece.) The sequence b = 0.5000 0 0 also provided states that, on the interval [0. .1], the B-spline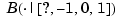 
can be written
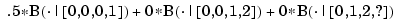
Cautionary Note
It is assumed that tx(.,k-1) < 0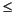 
tx(.,k) for splpp and tx(.,k-1) 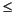0 < tx(.,k) for sprpp.
| | splinetool | spmak | |
