

| Spline Toolbox |   |
Put together a rational spline
Syntax
rp = rpmak(breaks,coefs)
rp = rpmak(breaks,coefs,d)
rs = rsmak(knots,coefs)
rs = rsmak(shape,parameters)
Description
Both rpmak and rsmak put together a rational spline from minimal information. rsmak is also equipped to provide rational splines that describe standard geometric shapes.
rpmak(breaks,coefs)
ppmak(breaks, coefs), -- except that the resulting ppform is tagged as a rational spline, i.e., as a rpform.
To describe what this means, let 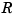 be the piecewise-polynomial put together by the command
be the piecewise-polynomial put together by the command ppmak(breaks,coefs), and let 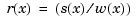 be the rational spline put together by the command
be the rational spline put together by the command rpmak(breaks,coefs). If v is the value of 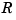 at
at 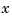 , then
, then v(1:end-1)/v(end) is the value of 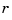 at
at 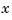 . In other words,
. In other words, 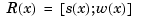 . Correspondingly, the dimension of the target of
. Correspondingly, the dimension of the target of 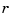 is one less than the dimension of the target of
is one less than the dimension of the target of 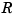 . In particular, the dimension (of the target) of
. In particular, the dimension (of the target) of 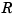 must be at least 2, i.e., the coefficients specified by
must be at least 2, i.e., the coefficients specified by coefs must be d-vectors with d > 1. See ppmak for how the input arrays breaks and coefs are being interpreted, hence how they are to be specified in order to produce a particular piecewise-polynomial.
rpmak(breaks,coefs,d)
ppmak(breaks,coefs,d+1), except that the resulting ppform is tagged as being a rpform. Note that the desire to have that optional third argument specify the dimension of the target requires different values for it in rpmak and ppmak for the same coefficient array coefs.
rsmak(knots,coefs)
spmak(knots,coefs). In particular, rsmak(knots,coefs) puts together a rational spline in B-form, i.e., it provides a rBform. See spmak for how the input arrays knots and coefs are being interpreted, hence how they are to be specified in order to produce a particular piecewise-polynomial.
rsmak(shape,parameters)
shape and the optional additional parameters. Specific choices are:
rsmak('circle',radius,center) rsmak('cone',radius,halfheight) rsmak('cylinder',radius,height) rsmak('southcap',radius,center)
From these, one may generate related shapes by affine transformations, with the help of fnbrk.
All fn... commands except fnint, fnder, fndir can handle rational splines.
Examples
both provide a description of the rational polynomial 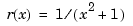 on the interval [-5 .. 5]. However, outside the interval [-5 .. 5], the function given by
on the interval [-5 .. 5]. However, outside the interval [-5 .. 5], the function given by runges is zero, while the rational spline given by rungep agrees with 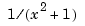 for every
for every 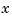 .
.
The figure of a rotated cone is generated by the commands
Figure 3-4: A Rotated Cone Given By a Rational Quadratic Spline
For further, illustrated examples, seeNURBS and Other Rational Splines.
See Also
 | ppmak | slvblk |  |