iofr, iofc (Robust Control Toolbox)

Robust Control Toolbox

iofr, iofc

Inner-outer factorization (row type).

Inner-outer factorization (column type).

Syntax

[ain,,ainp,,aout,] = iofr(c)(a,bcd)
[ssin,ssinp,ssout] = iofr(c)(ss)

Description
A square transfer function M(s) is outer if it is proper and stable and has an inverse that is also proper and stable. A transfer function 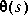of dimension
m by n is inner if it is stable and satisfies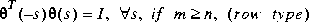

When 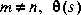has a complementary inner (or all-pass extension)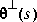

such that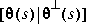 or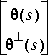 is square and inner.

Iofr computes an inner-outer factorization for a stable transfer function

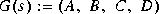for which m 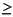n such that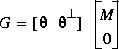

The output variables are defined as

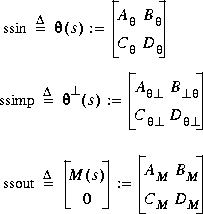
iofc computes an inner-outer factorization for the case of m < n via duality by applying iofr to G^T(s), then transposing the result.

Algorithm
iofr implements the algorithm described in [1], where it is shown that inner-outer factorization relates closely to the standard optimal LQ control problem as follows:

Given a transfer function G(s) := (A, B, C, D) of dimension m x n (m 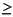n), the LQR optimal control u = -Fx = -R^-1(XB + N)^Tx stabilizes the system and minimizes the quadratic cost function

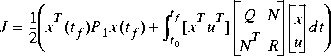
as , satisfies the algebraic Riccati equation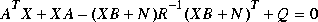

Moreover, the optimal return difference I + L(s) = I + F(Is - A) ^-1B satisfies the optimal LQ return difference equality:

where , and

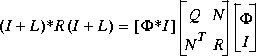
It may be easily shown [1] that the return difference equality implies that an inner-outer factorization of G(s) is given by

and

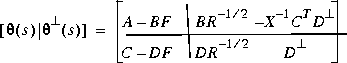
The variables X and F are computed via the MATLAB command:

[F,X] = lqr(A,B,Q,R,N) = lqr(A,B,C'*C,D'*D,C'*D).

The matrix X^-1 is a generalized inverse (e.g., a pseudoinverse). Although X may be singular,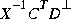

is well defined since the left null-space of

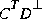includes the left null-space of X [1].

Iofc applies iofr to G^T(s), then transposes the result.

Limitations
The inner-outer factorization requires the system G(s) to be stable and to have neither poles nor transmission zeros on the j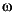-axis or at 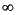. In particular D must have full column rank for iofr or full row rank for iofc.

See Also
sfl, sfr

References
[1] J. Doyle, Advances in Multivariable Control. Lecture Notes at ONR/Honeywell Workshop. Minneapolis, MN, Oct. 8-10, 1984.

[2] M. G. Safonov, E. A. Jonckheere, M. Verma and D. J. N. Limebeer, "Synthesis of Positive Real Multivariable Feedback Systems", Int. J. Control, vol. 45, no. 3, pp. 817-842, 1987.

interc lftf