SimPowerSystems

Modeling a Nonlinear Inductance

Consider an inductor of 2 henries designed to operate at a nominal voltage, Vnom = 120 V rms, and a nominal frequency, fnom = 60 Hz. From zero to 120 V rms the inductor has a constant inductance, L = 2 H. When voltage exceeds its nominal voltage, the inductor saturates and its inductance is reduced to Lsat = 0.5 H. The nonlinear flux-current characteristic is plotted in the next figure. Flux and current scales are in per units. The nominal voltage and nominal current are chosen as base values for the per-unit system.

Figure 1-23: Flux-Current Characteristic of the Nonlinear Inductance

The current i flowing in the inductor is a nonlinear function of flux linkage 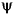that, in turn, is a function of v appearing across its terminals. These relations are given by the following equations:

The model of the nonlinear inductance can therefore be implemented as a controlled current source, where current i is a nonlinear function of voltage v, as shown.

Figure 1-24: Model of a Nonlinear Inductance

Figure 1-25 shows a circuit using a 2 H nonlinear inductance. The nonlinear inductance is connected in series with two voltage sources (an AC Voltage Source block of 120 volts rms, 60 Hz, and a DC Voltage Source block) and a 5 ohm resistor.

All the elements used to build the nonlinear model have been grouped in a subsystem named Nonlinear Inductance. The inductor terminals are labeled In and Out. Notice that a second output returning the flux has been added to the subsystem. This Simulink output can be used to observe the flux by connecting it to a Simulink Scope block.

The nonlinear model uses two powerlib blocks and two Simulink blocks. The two powerlib blocks are a Voltage Measurement block to read the voltage at the inductance terminals and a Controlled Current Source block. The direction of the arrow of the current source is oriented from input to output according to the model shown in Figure 1-24.

The two Simulink blocks are an Integrator block computing the flux from the voltage input and a Look-Up Table block implementing the saturation characteristic i = f(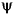) described by Figure 1-23.

Figure 1-25: Implementation of a Nonlinear Inductance

Two Fourier blocks from the Measurements library of powerlib_extras are used to analyze the fundamental component and the DC component of the current.

Using blocks of the powerlib and Simulink libraries, build the circuit of Figure 1-25. To implement the i =f(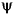) relation, specify the following vectors in the Look-Up Table block.

• Vector of input values (flux):
  [-1.25  -1  1 1.25 ] *(120*sqrt(2)/(2*60))
  Vector of output values (current):
  [-2 -1 1 2]*(120*sqrt(2)/(4*60))
  

Save your circuit as circuit7.

Set the following parameters for the two sources.

• AC source:  Peak amplitude = 120*sqrt(2) ; Phase = 90 degrees;
  Frequency = 60 Hz
  DC source: Amplitude = 0 V
  

Adjust the simulation time to 1.5 s and select the ode33tb integration algorithm with default parameters. Start the simulation.

As expected, the current and the flux are sinusoidal. Their peak values correspond to the nominal values.

Current and flux waveforms are shown.

Figure 1-26: Current and Flux Waveforms Obtained with VDC = 0 V and VDC = 1 V

Now change the DC voltage to 1 V and restart the simulation. Observe that the current is distorted. The 1 V DC voltage is now integrated, causing a flux offset, which makes the flux enter into the nonlinear region of the flux-current characteristic (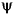 > 0.450 V.s) As a result of this flux saturation, the current contains harmonics. Zoom on the last three cycles of the simulation. The peak value of the current now reaches 0.70 A and the fundamental component has increased to 0.368 A. As expected, the DC component of the current is 1 V/ 0.5  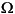= 0.2. The current and flux waveforms obtained with and without saturation are superimposed in Figure 1-26.

Session 8: Building and Customizing Nonlinear Models

Customizing Your Nonlinear Model