SimPowerSystems

Mathematical Model

The model considered is a single machine infinite bus (SMIB) system, as shown in the next figure. The machine is a synchronous generator driven by a hydraulic turbine.

Figure 2-16: Diagram of Case Study

The dynamic equations of the machine that are used to derive the linear feedback controller are for the three-phase Synchronous Machine block and the Hydraulic Turbine and Governor block (see Power System Block Reference). Because the synchronous machine is connected to an infinite bus, the dq terminal voltages v_d and v_q are constrained by the load equations. In the Park-transformed coordinates (rotor reference frame), v_d and v_q are expressed as

This equation can be combined with the complete model of the SMIB system in the nonlinear state-space form

F(x) and G(x) are given by

The explicit expressions of the coefficients A and g can be derived from the equations found in the Power System Block Reference under the Synchronous Machine block description. The other terms of the state-space equation are x, the vector of state variables, and u, the vector of control inputs. They are defined as follows:

The currents i_d, i_q and voltages v_d, v_q are the projection of the actual line currents and terminal voltages on the direct and quadrature axes (dq frame). i_fd and v_fd represent the field current and voltage. i_kq and i_kd represent the damper windings currents, and 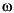the angular speed of the machine. 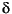is the electrical angle measured from a synchronously rotating frame. G and q are respectively the opening of the gate and the flow rate of the turbine. Finally, u_G is the voltage applied to the gate servomotor.

Synchronous Machine and Regulators

Feedback Linearization Design