Partial Differential Equation Toolbox

sptarn

Solve generalized sparse eigenvalue problem

Syntax

• [xv,lmb,iresult] = sptarn(A,B,lb,ub) 
  [xv,lmb,iresult] = sptarn(A,B,lb,ub,spd) 
  [xv,lmb,iresult] = sptarn(A,B,lb,ub,spd,tolconv) 
  [xv,lmb,iresult] = sptarn(A,B,lb,ub,spd,tolconv,jmax) 
  [xv,lmb,iresult] = sptarn(A,B,lb,ub,spd,tolconv,jmax,maxmul)
  

Description

[xv,lmb,iresult] = sptarn(A,B,lb,ub,spd,tolconv,jmax,maxmul) finds eigenvalues of the pencil (A - 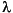B)x = 0 in interval [lb,ub]. (A matrix of linear polynomials Aij - 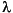Bij, A - 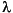B, is called a pencil.)

A and B are sparse matrices. lb and ub are lower and upper bounds for eigenvalues to be sought. We may have lb=-inf if all eigenvalues to the left of ub are sought, and rb=inf if all eigenvalues to the right of lb are sought. One of lb and ub must be finite. A narrower interval makes the algorithm faster. In the complex case, the real parts of lmb are compared to lb and ub.

xv are eigenvectors, ordered so that norm(a*xv-b*xv*diag(lmb)) is small. lmb is the sorted eigenvalues. If iresult>=0 the algorithm succeeded, and all eigenvalues in the intervals have been found. If iresult<0 the algorithm has not yet been successful, there may be more eigenvalues -- try with a smaller interval.

spd is 1 if the pencil is known to be symmetric positive definite (default 0).

tolconv is the expected relative accuracy. Default is 100*eps, where eps is the machine precision.

jmax is the maximum number of basis vectors. The algorithm needs jmax*n working space so a small value may be justified on a small computer, otherwise let it be the default value jmax=100. Normally the algorithm stops earlier when enough eigenvalues have converged.

maxmul is the number of Arnoldi runs tried. Must at least be as large as maximum multiplicity of any eigenvalue. If a small value of jmax is given, many Arnoldi runs are necessary. The default value is maxmul=n, which is needed when all the eigenvalues of the unit matrix are sought.

Algorithm

The Arnoldi algorithm with spectral transformation is used. The shift is chosen at ub, lb, or at a random point in interval (lb,ub) when both bounds are finite. The number of steps j in the Arnoldi run depends on how many eigenvalues there are in the interval, but it stops at j=min(jmax,n). After a stop, the algorithm restarts to find more Schur vectors in orthogonal complement to all those already found. When no more eigenvalues are found in lb < lmb <= ub, the algorithm stops. For small values of jmax, several restarts may be needed before a certain eigenvalue has converged. The algorithm works when jmax is at least one larger than the number of eigenvalues in the interval, but then many restarts are needed. For large values of jmax, which is the preferred choice, mul+1 runs are needed. mul is the maximum multiplicity of an eigenvalue in the interval.

Note    The algorithm works on nonsymmetric as well as symmetric pencils, but then accuracy is approximately tol times the Henrici departure from normality. The parameter spd is used only to choose between symmmd and colmmd when factorizing, the former being marginally better for symmetric matrices close to the lower end of the spectrum. In case of trouble, If convergence is too slow, try (in this order of priority): a smaller interval lb, ub a larger jmax a larger maxmul If factorization fails, try again with lb or ub finite. Then shift is chosen at random and hopefully not at an eigenvalue. If it fails again, check whether pencil may be singular. If it goes on forever, there may be too many eigenvalues in the strip. Try with a small value maxmul=2 and see which eigenvalues you get. Those you get are some of the eigenvalues, but a negative iresult tells you that you have not gotten them all. If memory overflow, try smaller jmax. The algorithm is designed for eigenvalues close to the real axis. If you want those close to the imaginary axis, try A=i*A. When spd=1, the shift is at lb so that advantage is taken of the faster factorization for symmetric positive definite matrices. No harm is done, but the execution is slower if lb is above the lowest eigenvalue.

See Also

pdeeig

Reference

Golub, Gene H., and Charles F. Van Loan, Matrix Computations, 2nd edition, Johns Hopkins University Press, Baltimore, MD, 1989.

Saad, Yousef, "Variations on Arnoldi's Method for Computing Eigenelements of Large Unsymmetric Matrices," Linear Algebra and its Applications, Vol. 34, 1980, pp. 269-295.

refinemesh

tri2grid