

| Partial Differential Equation Toolbox |   |
Syntax
Description
[v,l]=pdeeig(b,p,e,t,c,a,d,r)
produces the solution to the FEM formulation of the scalar PDE eigenvalue problem
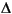 · (c
· (c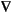 u) + au =
u) + au = 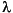 du on
du on 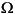
or the system PDE eigenvalue problem
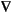 · (c
· (c 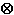
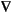 u) + au =
u) + au = 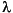 du on
du on 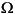
on a geometry described by p, e, and t, and with boundary conditions given by b.
r
is a two-element vector, indicating an interval on the real axis. (The left-hand side can be -Inf.) The algorithm returns all eigenvalues in this interval in l.
v
is an eigenvector matrix. For the scalar case each column in v is an eigenvector of solution values at the corresponding node points from p. For a system of dimension N with np node points, the first np rows of v describe the first component of v, the following np rows of v describe the second component of v, and so on. Thus, the components of v are placed in blocks v as N blocks of node point rows.
b
describes the boundary conditions of the PDE problem. b can be either a Boundary Condition matrix or the name of a Boundary M-file. The formats of the Boundary Condition matrix and Boundary M-file are described in the entries on assemb and pdebound, respectively. Note that the eigenvalue PDE problem is a homogeneous problem, i.e., only boundary conditions where g = 0 and r = 0 can be used. The nonhomogeneous part is removed automatically.
The geometry of the PDE problem is given by the mesh data p, e, and t. For details on the mesh data representation, see initmesh.
The coefficients c, a, d of the PDE problem can be given in a wide variety of ways. In the context of pdeeig the coefficients cannot depend on u nor t, the time. For a complete listing of all options, see assempde.
[v,l]=pdeeig(K,B,M,r)
produces the solution to the generalized sparse matrix eigenvalue problem
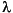 B´MBui u = Bui
B´MBui u = Bui
with Real(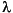 ) in the interval in r.
) in the interval in r.
Examples
Compute the eigenvalues less than 100 and corresponding eigenmodes for
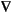 u =
u = 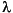 u,
u,
on the geometry of the L-shaped membrane. Then display the first and sixteenth eigenmodes.
[p,e,t]=initmesh('lshapeg'); [p,e,t]=refinemesh('lshapeg',p,e,t); [p,e,t]=refinemesh('lshapeg',p,e,t); [v,l]=pdeeig('lshapeb',p,e,t,1,0,1,[-Inf 100]); l(1) % first eigenvalue pdesurf(p,t,v(:,1)) % first eigenmode figure membrane(1,20,9,9) % the MATLAB function figure l(16) % sixteenth eigenvalue pdesurf(p,t,v(:,16)) % sixteenth eigenmode
Cautionary
In the standard case c and d are positive in the entire region. All eigenvalues are positive, and 0 is a good choice for a lower bound of the interval. The cases where either c or d is zero are discussed below.
K becomes singular, and the pencil (K,M) has many zero eigenvalues. With an interval containing zero, pdeeig goes on for a very long time to find all the zero eigenvalues. Choose a positive lower bound away from zero but below the smallest nonzero eigenvalue.
Some of the awkward cases are detected by pdeeig. If the shifted matrix is singular, another shift is attempted. If the matrix with the new shift is still singular a good guess is that the entire pencil (K,M) is singular.
If you try any problem not belonging to the standard case, you must use your knowledge of the original physical problem to interpret the results from the computation.
See Also
 | pdecont | pdeellip |  |