Partial Differential Equation Toolbox

pdenonlin

Solve nonlinear PDE problem

Syntax

• [u,res]=pdenonlin(b,p,e,t,c,a,f) 
  [u,res]=pdenonlin(b,p,e,t,c,a,f,'PropertyName',
  'PropertyValue',...)
  

Description

[u,res]=pdenonlin(b,p,e,t,c,a,f) solves the nonlinear PDE scalar PDE problem

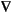- · (c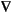u) + au = f on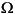

or the nonlinear system PDE problem

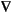- · (c 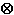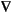u) + au = f on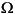

where the coefficients c, a, and f may depend on u. The algorithm solves the equation by using damped Newton iteration with the Armijo-Goldstein line search strategy.

The solution u is represented as the solution vector u. For details on the representation of the solution vector, see assempde. res is the norm of the Newton step residuals.

The triangular mesh of the PDE problem is given by the mesh data p, e, and t. For details on the mesh data representation, see initmesh.

b describes the boundary conditions of the PDE problem. b can be either a Boundary Condition matrix or the name of a Boundary M-file. The formats of the Boundary Condition matrix and Boundary M-file are described in the entries on assemb and pdebound, respectively, respectively. Note that for the general call to pdebound the boundary conditions can also depend on u. A fixed-point iteration strategy is employed to solve for the nonlinear boundary conditions.

The coefficients c, a, f of the PDE problem can be given in a wide variety of ways. In the context of pdenonlin the coefficients can depend on u. The coefficients cannot depend on t, the time. For a complete listing of all format options, see assempde.

The solver can be fine-tuned by setting some of the options described below

Property Name	Property Value	Default	Description
Jacobian	fixed|lumped|full	fixed	Approximation of Jacobian
U0	string or numeric	0	Initial solution guess
Tol	positive scalar	1e-4	Residual size at termination
MaxIter	positive integer	25	Maximum Gauss-Newton iterations
MinStep	positive scalar	1/2^16	Minimum damping of search direction
Report	on|off	off	Print convergence information
Norm	string or numeric	Inf	Residual norm

There are three methods currently implemented to compute the Jacobian:

• Numerical evaluation of the full Jacobian based on the sparse version of the function numjac
• A "lumped" approximation described in The Finite Element Method, based on the numerical differentiation of the coefficients
• A fixed-point iteration matrix where the Jacobian is approximated by the stiffness matrix

Select the desired method by setting the Jacobian property to full, lumped, or fixed, bearing in mind that the more precise methods are computationally more expensive.

U0 is the starting guess that can be given as an expression, a generic scalar, or a vector. By default it is set to 0, but this is useless in problems such as 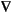(1/u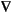u) = 0 with Dirichlet boundary conditions u = ex+y. Tol fixes the exit criterion from the Gauss-Newton iteration, i.e., the iterations are terminated when the residual norm is less than Tol. The norm in which the residual is computed is selected through Norm. This can be any admissible MATLAB vector norm or energy for the energy norm.

MaxIter and MinStep are safeguards against infinite Gauss-Newton loops and they bound the number of iterations and the step size used in each iteration. Setting Report to on forces printing of convergence information.

Diagnostics

If the Newton iteration does not converge, the error message Too many iterations or Stepsize too small is displayed. If the initial guess produces matrices containing NaN or Inf elements, the error message Unsuitable initial guess U0 (default: U0=0) is printed.

See Also

assempde, pdebound

pdemesh

pdeplot