Partial Differential Equation Toolbox

adaptmesh

Adaptive mesh generation and PDE solution

Syntax

• [u,p,e,t]=adaptmesh(g,b,c,a,f) 
  [u,p,e,t]=adaptmesh(g,b,c,a,f,'PropertyName',PropertyValue,)
  

Description

[u,p,e,t]=adaptmesh(g,b,c,a,f,'PropertyName',PropertyValue,) performs adaptive mesh generation and PDE solution. Optional arguments are given as property name/property value pairs.

The function produces a solution u to the elliptic scalar PDE problem

- · (cu) + au = f on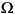

or the elliptic system PDE problem

- · (c u) + au = f on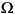

with the problem geometry and boundary conditions given by g and b. The mesh is described by the p, e, and t.

The solution u is represented as the solution vector u. For details on the representation of the solution vector, see assempde.

The algorithm works by solving a sequence of PDE problems using refined triangular meshes. The first triangular mesh generation is obtained either as an optional argument to adaptmesh or by a call to initmesh without options. The following generations of triangular meshes are obtained by solving the PDE problem, computing an error estimate, selecting a set of triangles based on the error estimate, and then finally refining these triangles. The solution to the PDE problem is then recomputed. The loop continues until no triangles are selected by the triangle selection method, or until the maximum number of triangles is attained, or until the maximum number of triangle generations has been generated.

g describes the decomposed geometry of the PDE problem. g can either be a Decomposed Geometry matrix or the name of a Geometry M-file. The formats of the Decomposed Geometry matrix and Geometry M-file are described in the entries on decsg and pdegeom, respectively.

b describes the boundary conditions of the PDE problem. b can be either a Boundary Condition matrix or the name of a Boundary M-file. The formats of the Boundary Condition matrix and Boundary M-file are described in the entries on assemb and pdebound, respectively.

The adapted triangular mesh of the PDE problem is given by the mesh data p, e, and t. For details on the mesh data representation, see initmesh.

The coefficients c, a, and f of the PDE problem can be given in a wide variety of ways. In the context of adaptmesh the coefficients can depend on u if the nonlinear solver is enabled using the property nonlin. The coefficients cannot depend on t, the time. For a complete listing of all options, see assempde.

The table below lists the property name/property value pairs, their default values, and descriptions of the properties.

Property	Property	Default	Description
Maxt	positive integer	inf	Maximum number of new triangles
Ngen	positive integer	10	Maximum number of triangle generations
Mesh	p1, e1, t1	initmesh	Initial mesh
Tripick	MATLAB function	pdeadworst	Triangle selection method
Par	numeric	0.5	Function parameter
Rmethod	longest|regular	longest	Triangle refinement method
Nonlin	on|off	off	Use nonlinear solver
Toln	numeric	1e-4	Nonlinear tolerance
Init	u0	0	Nonlinear initial value
Jac	fixed|lumped|full	fixed	Nonlinear Jacobian calculation
norm	numeric|inf|energy	inf	Nonlinear residual norm

Par is passed to the Tripick function. (The Tripick function is described below.) Normally it is used as tolerance of how well the solution fits the equation.

No more than Ngen successive refinements are attempted. Refinement is also stopped when the number of triangles in the mesh exceeds Maxt.

p1, e1, and t1 are the input mesh data. This triangular mesh is used as starting mesh for the adaptive algorithm. For details on the mesh data representation, see initmesh. If no initial mesh is provided, the result of a call to initmesh with no options is used as the initial mesh.

The triangle selection method, Tripick, is a user-definable triangle selection method. Given the error estimate computed by the function pdejmps, the triangle selection method selects the triangles to be refined in the next triangle generation. The function is called using the arguments p, t, cc, aa, ff, u, errf, and par. p and t represent the current generation of triangles, cc, aa, and ff are the current coefficients for the PDE problem, expanded to triangle midpoints, u is the current solution, errf is the computed error estimate, and par, the function parameter, given to adaptmesh as optional argument. The matrices cc, aa, ff, and errf all have Nt columns, where Nt is the current number of triangles. The number of rows in cc, aa, and ff are exactly the same as the input arguments c, a, and f. errf has one row for each equation in the system. There are two standard triangle selection methods in the toolbox -- pdeadworst and pdeadgsc. pdeadworst selects triangles where errf exceeds a fraction (default: 0.5) of the the worst value, and pdeadgsc selects triangles using a relative tolerance criterion.

The refinement method is either longest or regular. For details on the refinement method, see refinemesh.

The adaptive algorithm can also solve nonlinear PDE problems. For nonlinear PDE problems, the Nonlin parameter must be set to on. The nonlinear tolerance Toln, nonlinear initial value u0, nonlinear Jacobian calculation Jac, and nonlinear residual norm Norm are passed to the nonlinear solver pdenonlin. For details on the nonlinear solver, see pdenonlin .

Examples

Solve the Laplace equation over a circle sector, with Dirichlet boundary conditions u = cos(2/3atan2(y,x)) along the arc, and u = 0 along the straight lines, and compare to the exact solution. We refine the triangles using the worst error criterion until we obtain a mesh with at least 500 triangles:

• [u,p,e,t]=adaptmesh('cirsg','cirsb',1,0,0,'maxt',500,... 
                         'tripick','pdeadworst','ngen',inf); 
  x=p(1,:); y=p(2,:); 
  exact=((x.^2+y.^2).(1/3).*cos(2/3*atan2(y,x)))'; 
  max(abs(u-exact)) 
  ans = 
      0.0058 
  size(t,2) 
  ans = 
      534 
  pdemesh(p,e,t)
  
  
  
  

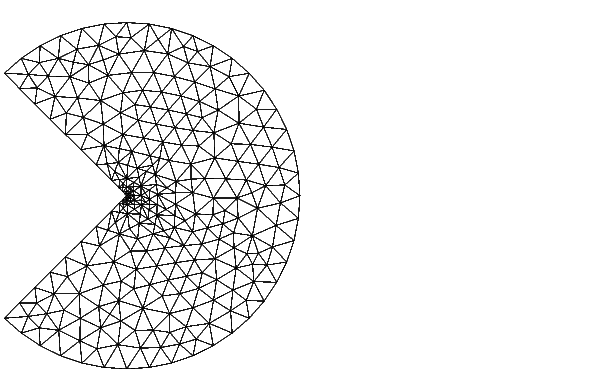
The maximum absolute error is 0.0058, with 534 triangles. We test how many refinements we have to use with a uniform triangle net:

• [p,e,t]=initmesh('cirsg'); 
  [p,e,t]=refinemesh('cirsg',p,e,t); 
  u=assempde('cirsb',p,e,t,1,0,0); 
  x=p(1,:); y=p(2,:); 
  exact=((x.^2+y.^2).^(1/3).*cos(2/3*atan2(y,x)))'; 
  max(abs(u-exact)) 
  ans =
         0.0085 
  size(t,2) 
  ans =
         1640 
  [p,e,t]=refinemesh('cirsg',p,e,t); 
  u=assempde('cirsb',p,e,t,1,0,0); 
  x=p(1,:); y=p(2,:); 
  exact=((x.^2+y.^2).^(1/3).*cos(2/3*atan2(y,x)))'; 
  max(abs(u-exact)) 
  ans =
         0.0054 
  size(t,2) 
  ans =
         6560 
  pdemesh(p,e,t)
  

Thus, with uniform refinement, we need 6560 triangles to achieve better absolute error than what we achieved with the adaptive method. Note that the error is reduced only by 0.6 when the number of elements in quadrupled by the uniform refinement. For a problem with regular solution, we expect a O(h²) error, but this solution is singular since u 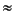r^1/3 at the origin.

Diagnostics

Upon termination, one of the following messages is displayed:

• Adaption completed (This means that the Tripick function returned zero triangles to refine.)
• Maximum number of triangles obtained
• Maximum number of refinement passes obtained

See Also

initmesh, refinemesh, assempde, pdeadgsc, pdeadworst, pdejmps

Functions -- Alphabetical List

assema