

| Partial Differential Equation Toolbox |   |
The Hyperbolic Equation
Using the same ideas as for the parabolic equation, hyperbolic implements the numerical solution of
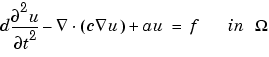
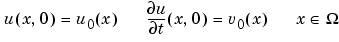
and usual boundary conditions. In particular, solutions of the equation
utt - c u = 0 are waves moving with speed
u = 0 are waves moving with speed  .
.
Using a given triangulation of 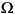 , the method of lines yields the second order ODE system
, the method of lines yields the second order ODE system
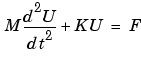
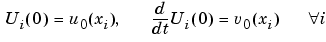
after we eliminate the unknowns fixed by Dirichlet boundary conditions. As before, the stiffness matrix K and the mass matrix M are assembled with the aid of the function assempde from the problems
 · (c
· (c u) + au = f and -
u) + au = f and - · (0
· (0 u) + du = 0
u) + du = 0
 | The Parabolic Equation | The Eigenvalue Equation |  |