

| Partial Differential Equation Toolbox |   |
The Parabolic Equation
The elliptic solver allows other types of equations to be more or less easily implemented. Below we show how the parabolic equation can be reduced to solving elliptic equations. This is done by the toolbox function parabolic.
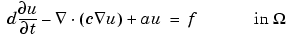
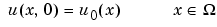
and boundary conditions of the same kind as for the elliptic equation on  .
.
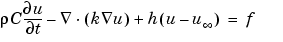
in the presence of distributed heat loss to the surroundings.  is the density, C thermal capacity, k thermal conductivity, h film coefficient, u
is the density, C thermal capacity, k thermal conductivity, h film coefficient, u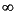 ambient temperature, and f heat source.
ambient temperature, and f heat source.
For time-independent coefficients, the steady state solution of the equation is the solution to our standard elliptic equation
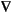 · (c
· (c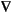 u) + au = f
u) + au = f
Assuming a triangular mesh on 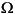 and at any time t
and at any time t  0, expand the solution to the PDE (as a function of x) in the Finite Element Method basis:
0, expand the solution to the PDE (as a function of x) in the Finite Element Method basis:
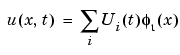
Plugging the expansion into the PDE, multiplying with a test function 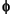 j, integrating over
j, integrating over 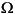 , and applying Green's formula and the boundary conditions yield
, and applying Green's formula and the boundary conditions yield
In matrix notation, we have to solve the linear, large and sparse ODE system
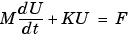
This method is traditionally called method of lines semidiscretization.
Solving the ODE with the initial value
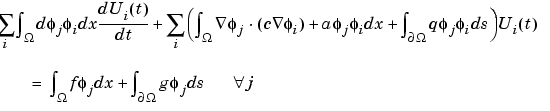
yields the solution to the PDE at each node xi and time t. Note that K and F are the stiffness matrix and the right-hand side of the elliptic problem
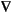 · (c
· (c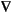 u) + au = f in
u) + au = f in 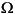
with the original boundary conditions while M is just the mass matrix of the problem
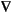 · (0
· (0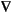 u) + du = 0 in
u) + du = 0 in 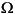
When the Dirichlet conditions are time dependent, F contains contributions from time derivatives of h and r. These derivatives are evaluated by finite differences of the user-specified data.
The ODE system is ill conditioned. Explicit time integrators are forced by stability requirements to very short time steps while implicit solvers can be expensive since they solve an elliptic problem at every time step. The numerical integration of the ODE system is performed by the MATLAB ODE Suite functions, which are efficient for this class of problems. The time step is controlled to satisfy a tolerance on the error, and factorizations of coefficient matrices are performed only when necessary. When coefficients are time dependent, the necessity of reevaluating and refactorizing the matrices each time step may still make the solution time consuming, although parabolic reevaluates only that which varies with time. In certain cases a time-dependent Dirichlet matrix h(t) may cause the error control to fail, even if the problem is mathematically sound and the solution u(t) is smooth. This can happen because the ODE integrator looks only at the reduced solution v with u = Bv + ud. As h changes, the pivoting scheme employed for numerical stability may change the elimination order from one step to the next. This means that B,v and ud all change discontinuously, although u itself does not.
 | The Elliptic System | The Hyperbolic Equation |  |