Partial Differential Equation Toolbox

PDE Menu

PDE Mode	Enter the partial differential equation mode.
Show Subdomain Labels	Toggle the labeling of the subdomains on/off. The subdomains are labeled using the subdomain numbering in the decomposed geometry matrix.
PDE Specification . . .	Open dialog box for entering PDE coefficients and types.
Export PDE Coefficients . . .	Export current PDE coefficients to the main workspace. The resulting workspace variables are strings.

PDE Specification . . .

PDE Specification . . . opens a dialog box where you enter the type of partial differential equation and the applicable parameters. The dimension of the parameters is dependent on the dimension of the PDE. The description below applies to scalar PDEs. If a nongeneric application mode is selected, application-specific PDEs and parameters replace the standard PDE coefficients. For a thorough description of the different application modes, see Application Modes.

Each of the coefficients c, a, f, and d can be given as a valid MATLAB expression for computing coefficient values at the triangle centers of mass. The following variables are available:

• x and y: The x- and y-coordinates
• u: The solution
• ux, uy: The x and y derivatives of the solution
• t: The time

Note    If the PDE coefficient is a function of the solution u or its derivatives ux and uy, you must use the nonlinear solver. If the PDE coefficient is a function of the time t, you must choose a parabolic or hyperbolic PDE.

You can also enter the name of a user-defined MATLAB function that accepts the arguments (p,t,u,time). For an example, type the function circlef.

c can be a scalar or a 2-by-2 matrix. The matrix c can be used to model, e.g., problems with anisotropic material properties.

If c contains two rows, they are the c_1,1 and c_2,2 elements of a 2-by-2 symmetric matrix

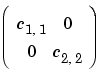
If c contains three rows, they are the c_1,1, c_1,2, and c_2,2 elements of a 2-by-2 symmetric matrix (c_2,1 = c_1,2)

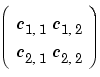
If c contains four rows, they are the c_1,1, c_2,1, c_1,2, and c_2,2 elements of the 2-by-2 matrix above.

The available types of PDEs are

• Elliptic. The basic form of the elliptic PDE is

• The parameter d does not apply to the elliptic PDE.

• Parabolic. The basic form of the parabolic PDE is

• with initial values u0 = u(t₀).

• Hyperbolic. The basic form of the hyperbolic PDE is

• with initial values u0 = u(t₀) and ut0 =
  
  (t₀)

• Eigenmodes. The basic form of the PDE eigenvalue problem is

• The parameter f does not apply to the eigenvalue PDE.

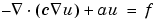
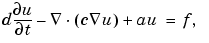
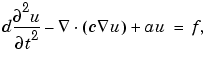
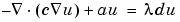
In the system case, c is a rank four tensor, which can be represented by four 2-by-2 matrices, c11, c12, c21, and c22. They can be entered as one, two, three, or four rows -- see the scalar case above. a and d are 2-by-2 matrices, and f is a 2-by-1 vector. The PDE Specification dialog box for the system case is shown below.

Boundary Menu

Mesh Menu