| Optimization Toolbox | |
Nonlinear Minimization with a Dense but Structured Hessian and Equality Constraints
The fmincon and fminunc large-scale methods can solve problems where the Hessian is dense but structured. For these problems, fmincon and fminunc do not compute H*Y with the Hessian H directly, as they do for medium-scale problems and for large-scale problems with sparse H, because forming H would be memory-intensive. Instead, you must provide fmincon or fminunc with a function that, given a matrix Y and information about H, computes W = H*Y.
In this example, the objective function is nonlinear and linear equalities exist so fmincon is used. The objective function has the structure
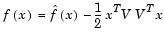
where V is a 1000-by-2 matrix. The Hessian of f is dense, but the Hessian of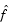 
is sparse. If the Hessian of 
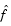is 
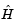, then 
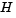, the Hessian of 
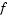, is
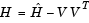
To avoid excessive memory usage that could happen by working with H directly, the example provides a Hessian multiply function, hmfleq1. This function, when passed a matrix Y, uses sparse matrices Hinfo, which corresponds to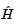 
, and V to compute the Hessian matrix product
In this example, the Hessian multiply function needs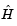 
and V to compute the Hessian matrix product. V is a constant, so V can be passed as an additional parameter to fmincon. Then fmincon passes V as an additional parameter to hmfleq1.
However,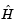 
is not a constant and must be computed at the current x. You can do this by computing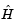 
in the objective function and returning 
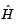as Hinfo in the third output argument. By using optimset to set the 'Hessian' options to 'on', fmincon knows to get the Hinfo value from the objective function and pass it to the Hessian multiply function hmfleq1.
Step 1: Write an M-file brownvv.m that computes the objective function, the gradient, and the sparse part of the Hessian.
The example passes brownvv to fmincon as the objective function. The brownvv.m file is long and is not included here. You can view the code with the command
Because brownvv computes the gradient and part of the Hessian as well as the objective function, the example (Step 3) uses optimset to set the GradObj and Hessian parameters to 'on'.
Step 2: Write a function to compute Hessian-matrix products for H given a matrix Y.
Now, define a function hmfleq1 that uses Hinfo, which is computed in brownvv, and V, which the example passes to fmincon as an additional parameter, to compute the Hessian matrix product W where W = H*Y = (Hinfo - V*V')*Y. This function must have the form
The first argument must be the same as the third argument returned by the objective function brownvv. The second argument to the Hessian multiply function is the matrix Y (of W = H*Y).
Because fmincon expects the second argument Y to be used to form the Hessian matrix product, Y is always a matrix with n rows where n is the number of dimensions in the problem. The number of columns in Y can vary. Finally, any additional parameters passed to fmincon are passed to the Hessian multiply function, so hmfleq1 must accept the same additional parameters, e.g., the matrix V:
function W = hmfleq1(Hinfo,Y,V); %HMFLEQ1 Hessian-matrix product function for BROWNVV objective. % W = hmfleq1(Hinfo,Y,V) computes W = (Hinfo-V*V')*Y % where Hinfo is a sparse matrix computed by BROWNVV % and V is a 2 column matrix. W = Hinfo*Y - V*(V'*Y);
Step 3: Call a nonlinear minimization routine with a starting point and linear equality constraints.
Load the problem parameter, V, and the sparse equality constraint matrices, Aeq and beq, from fleq1.mat, which is available in the Optimization Toolbox. Use optimset to set the GradObj and Hessian options to 'on' and to set the HessMult option to a function handle that points to hmfleq1. Call fmincon with objective function brownvv and with V as an additional parameter:
load fleq1 % Get V, Aeq, beq n = 1000; % problem dimension mtxmpy = @hmfleq1; % Function handle to function hmfleq1 xstart = -ones(n,1); xstart(2:2:n,1) = ones(length(2:2:n),1); options = optimset('GradObj','on','Hessian','on',... 'HessMult',mtxmpy,'Display','iter'); [x,fval,exitflag,output] = fmincon(@brownvv,xstart,[],[],... Aeq,beq,[],[],[],... options,V);
Note
Type [fval,exitflag,output] = runfleq1 to run the preceding code. This command displays the values for fval, exitflag, and output, as well as the following iterative display.
|
Because the iterative display was set using optimset, the results displayed are
Norm of First-order Iteration f(x) step optimality CG-iterations 1 1997.07 1 555 0 2 1072.56 6.31716 377 1 3 480.232 8.19554 159 2 4 136.861 10.3015 59.5 2 5 44.3708 9.04697 16.3 2 6 44.3708 100 16.3 2 7 44.3708 25 16.3 0 8 -8.90967 6.25 28.5 0 9 -318.486 12.5 107 1 10 -318.486 12.5 107 1 11 -415.445 3.125 73.9 0 12 -561.688 3.125 47.4 2 13 -785.326 6.25 126 3 14 -785.326 4.30584 126 5 15 -804.414 1.07646 26.9 0 16 -822.399 2.16965 2.8 3 17 -823.173 0.40754 1.34 3 18 -823.241 0.154885 0.555 3 19 -823.246 0.0518407 0.214 5 2 -823.246 0.00977601 0.00724 6 Optimization terminated successfully: Relative function value changing by less than OPTIONS.TolFun
Convergence is rapid for a problem of this size with the PCG iteration cost increasing modestly as the optimization progresses. Feasibility of the equality constraints is maintained at the solution
Preconditioning
In this example, fmincon cannot use H to compute a preconditioner because H only exists implicitly. Instead of H, fmincon uses Hinfo, the third argument returned by brownvv, to compute a preconditioner. Hinfo is a good choice because it is the same size as H and approximates H to some degree. If Hinfo were not the same size as H, fmincon would compute a preconditioner based on some diagonal scaling matrices determined from the algorithm. Typically, this would not perform as well.
| | Nonlinear Minimization with Equality Constraints | Quadratic Minimization with Bound Constraints | |