Model Predictive Control Toolbox

Calculates the MIMO step response of a model in the MPC tf format. The resulting step response is in the MPC step format.

Syntax

• plant = tfd2step(tfinal,delt2,nout,g1) 
  plant = tfd2step(tfinal,delt2,nout,g1,...,g25) 
  

Description
The input variables are as follows:

tfinal
Truncation time for step response.

delt2
Desired sampling period for step response.

nout
Output stability indicator. For stable systems, this argument is set equal to the number of outputs, ny. For systems with one or more integrating outputs, this argument is a column vector of length ny with nout(i)=0 indicating an integrating output and nout(i)=1 indicating a stable output.

g1, g2,...gN
A sequence of N transfer functions in the tf format (see tf format section), where N 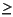1. These are assumed to be the individual elements of a transfer-function matrix:

Thus it should be clear that N must be an integer multiple (nu) of the number of outputs, ny.

tfd2step assumes that you are supplying the transfer functions in a column-wise order. In other words, you should first give the ny transfer functions for input 1 (g_1,1 to gny, 1), then the ny transfer functions for input 2 (g_1,2 to gny, 2), etc.

The output variable plant is the calculated step response of the ny outputs with respect to all inputs. The format is as described in the step section.

Example
Consider the linear system:

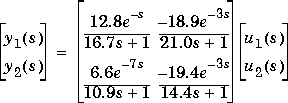
which is the same as that considered in the mpcsim example. We build the individual tf format models, then calculate and plot the MIMO step response.

• g11=poly2tfd(12.8,[16.7 1],0,1);
  g21=poly2tfd(6.6,[10.9 1],0,7);
  g12=poly2tfd(-18.9,[21.0 1],0,3);
  g22=poly2tfd(-19.4,[14.4 1],0,3);
  delt=3; ny=2; tfinal=90;
  plant=tfd2step(tfinal,delt,ny,g11,g21,g12,g22,gw1,gw2); 
  plotstep(plant)
  

Restriction
The current limit on the number of input transfer functions is N = 25.

See Also
mod2step, plotstep, ss2step

tfd2mod, tf format

th2mod, theta format