dlqe2 (Model Predictive Control Toolbox)

Model Predictive Control Toolbox

dlqe2

Solves the discrete Riccati equation by an iterative method to determine the optimal steady-state gain (and optional covariance matrices) for a discrete Kalman filter or state estimator.

Syntax

k = dlqe2(phi,gamw,c,q,r) 
[k,m,p] = dlqe2(phi,gamw,c,q,r)

Description
Filter form:

Consider the state-space description:

where x is a vector of n state variables, u contains nu known inputs, 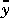is a vector of ny measured outputs, y is the noise-free output, w is a vector of nw unmeasured disturbance inputs, z is a vector of ny measurement noise inputs, and 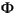, 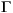u, 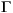w,C and D are constant matrices. We assume that w and z are stationary random-normal signals (white noise) with covariances

{

(

)

(

)} =

{

(

)

(

)} =

₁₂

= 0

{

(

)

(

)} =

The steady-state Kalman filter is

where 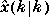is the estimate of x(k) based on the measurements available at period k, 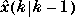is that based on the measurements available at period
k - 1, etc. Note that 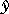is an estimate of the noise-free output, 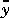. The steady-state Kalman gain, K, is the solution of

where M and P may be interpreted as the expected covariance of the errors in the state estimates before and after the measurement update, respectively, i.e.,

where, by definition,

The dlqe2 function takes 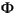, 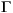u, C, R, and Q as inputs and calculates K, M, and P. The last two output arguments are optional.

Note that the input and output arguments are identical to those for dlqe in the Control Toolbox. The advantage of dlqe2 is that it can handle a singular state-transition matrix (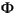), e.g., for systems with time delay.

Predictor form:

You can also use dlqe2 to calculate a state-estimator in the predictor form:

The relationship between Kp, the estimator gain for the predictor form, and K as calculated by dlqe2 is:

The matrix M calculated by dlqe2 is the expected covariance of the errors in .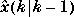

Algorithm
dlqe2 calls dareiter, which solves the discrete algebraic Riccati equation using an iterative doubling algorithm.

Example
Consider a system represented by the block diagram:

where Gu and Gw are first-order, discrete-time transfer functions.

and the statistics of the unmeasured inputs are Q = 2, R = 1.

We use the appropriate MPC Toolbox functions to build a model of the system, then calculate the optimal gain:

delt=2; ny=1;
gu=poly2tfd(0.2,[1 -0.8],delt);
Gw=poly2tfd(0.3,[1 -0.95],delt);
[phi,gam,c,d]=mod2ss(tfd2mod(delt,ny,gu,Gw));
k=dlqe2(phi,gam(:,2),c,2,1)

The result is:

```
k = 0 
    1.0619
```

Note that the gain for the first state is zero since this corresponds to the state of Gu, which is unaffected by the disturbance, w. Also notice that in the composite system, the second column of gam is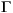

w. This is because of the order in which gu and Gw were specified as inputs to the tfd2mod function.

See Also
smpcest

cp2dp imp2step