Model Browser User's Guide

Box-Cox Transformation

You might want to transform a response feature either to correct for nonnormality and/or a heteroscedastic variance structure. A useful class of transformations for this purpose is the power transform y, where is a parameter to be determined. Box and Cox (1964) showed how and the regression coefficients themselves could be estimated simultaneously using the method of maximum likelihood. The procedure consists of conducting a standard least squares fit using

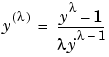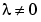
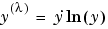• for

• for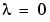

where the so called geometric mean of the observations is given by

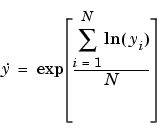
The maximum likelihood estimate of corresponds to the value for which the SSE() from the fitted model is a minimum. This value of is determined by fitting a model (assumed throughout to be defined by the regression matrix for the full model - X) for various levels of and choosing the value corresponding to the minimum SSE(). A plot of SSE() versus is often used to facilitate this choice.

The parameter is swept between the range of -3 to 3 in increments of 0.5.

• You can enter a value for lambda in the edit box that approaches the point on the plot with the smallest SSE.

Although SSE() is a continuous function of , simple choices for are recommended. This is because the practical difference between 0.5 and 0.593, say, is likely to be very small but a simple transform like 0.5 is much easier to interpret.

You can also find an approximate 100(1-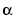) confidence interval on l by computing

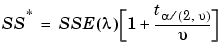
where 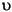is the number of residual degrees of freedom equal to (N-q).

In this formula is understood to be the value that minimizes SSE(). Note that this confidence interval might encompass more than one incremental value for . In this case, any of these values is as valid as any other and you can select any of these transformations from which to develop trial models.

• You should always look at the residuals plots at the top to see the effect of different transforms.
• You can create several child nodes of a single model and choose different transforms for each in order to compare them using the rest of the Model Browser tools.

For the sake of clarity, consider the example following, which illustrates the outcome of applying the Box-Cox method.

The preceding example shows the results of applying the Box-Cox algorithm to a polyspline torque model.

In this example the minimum value of SSE() occurs near to =0. The minimum is marked in green. The 95% confidence limit has been calculated and drawn on the figure as a red solid line. It is apparent in this example that, after rounding to the nearest incremental value contained within the confidence interval, any in the range 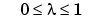is appropriate. Of the three possible increments, 0, 0.5, and 1, = 0.5 is the closest to the minimum SSE.

You can select any point on the plot by clicking. The chosen point (current lambda) is then outlined in red. You can also enter values of lambda directly in the edit box and press Return.

Stepwise Table

Linear Model Statistics Displays