Technical Documents (Model Browser User's Guide)

Model Browser User's Guide

PRESS Statistic

With n runs in the data set, the model equation is fitted to n-1 runs and a prediction taken from this model for the remaining one. The difference between the recorded data value and the value given by the model (at the value of the omitted run) is called a prediction residual. PRESS is the sum of squares of the prediction residuals. The square root of PRESS/n is PRESS RMSE (root mean square prediction error).

Note that the prediction residual is different from the ordinary residual, which is the difference between the recorded value and the value of the model when fitted to the whole data set.

The PRESS statistic gives a good indication of the predictive power of your model, which is why minimizing PRESS is desirable. It is useful to compare PRESS RMSE with RMSE as this can indicate problems with overfitting. RMSE is minimized when the model gets very close to each data point; "chasing" the data will therefore improve RMSE. However, chasing the data can sometimes lead to strong oscillations in the model between the data points; this behavior can give good values of RMSE but is not representative of the data and does not give reliable prediction values where you do not already have data. The PRESS RMSE statistic guards against this by testing how well the current model would predict each of the points in the data set (in turn) if they were not included in the regression. To get a small PRESS RMSE usually indicates that the model is not overly sensitive to any single data point.

For more information, see Stepwise Regression Techniques and Definitions.

Note that calculating PRESS for the two-stage model applies the same principle (fitting the model to n-1 runs and taking a prediction from this model for the remaining one) but in this case the predicted values are first found for response features instead of data points. The predicted value, omitting each test in turn, for each response feature is estimated. The predicted response features are then used to reconstruct the local curve for the test and this curve is used to obtain the two-stage predictions. This is applied as follows:

To calculate two stage PRESS:

For each test, S, do the following steps:

For each of the response features, calculate what the response feature predictions would be for S (with the response features for S removed from the calculation).
This gives a local prediction curve C based on all tests except S.
For each data point in the test, calculate the difference between the observed value and the value predicted by C.

Repeat for all tests.
Sum the square of all of the differences found and divide by the total number of data points.

Pooled Statistics

Local RMSE

Root mean squared error, using the local model fit to the data for the displayed test. The divisor used for RMSE is the number of observations minus the number of parameters.

Two-Stage RMSE

Root mean squared error, using the two-stage model fit to the data for the displayed test. You want this error to be small for a good model fit.

PRESS RMSE

Root mean squared error of predicted errors, see PRESS Statistic above. The divisor used for PRESS RMSE is the number of observations. Not displayed for MLE models because the simple univariate formula cannot be used.

Two-Stage T^2

T^2 is a normalized sum of squared errors for all the response features models. You can see the basic formula on the Likelihood view of the Model Selection window.

Where

, where C_iis the local covariance for test i. See blockdiag diagram following.

A large T^2 value indicates that there is a problem with the response feature models.

-log L

Log-likelihood function: the probability of a set of observations given the value of some parameters. You want the likelihood to be large, tending towards -infinity, so large negative is good.

For n observations x₁,x₂,..x_n, with probability distribution , the likelihood is

This is the basis of Maximum Likelihood Estimation.

which is the same as

This assumes a normal distribution.

You can view plots of -log L in the Model Selection window, see Likelihood View.

Local RMSE	Root mean squared error, using the local model fit to the data for the displayed test. The divisor used for RMSE is the number of observations minus the number of parameters.
Two-Stage RMSE	Root mean squared error, using the two-stage model fit to the data for the displayed test. You want this error to be small for a good model fit.
PRESS RMSE	Root mean squared error of predicted errors, see PRESS Statistic above. The divisor used for PRESS RMSE is the number of observations. Not displayed for MLE models because the simple univariate formula cannot be used.
Two-Stage T^2	T^2 is a normalized sum of squared errors for all the response features models. You can see the basic formula on the Likelihood view of the Model Selection window. Where , where C_iis the local covariance for test i. See blockdiag diagram following. A large T^2 value indicates that there is a problem with the response feature models.
-log L	Log-likelihood function: the probability of a set of observations given the value of some parameters. You want the likelihood to be large, tending towards -infinity, so large negative is good. For n observations x₁,x₂,..x_n, with probability distribution , the likelihood is This is the basis of Maximum Likelihood Estimation. which is the same as This assumes a normal distribution. You can view plots of -log L in the Model Selection window, see Likelihood View.

To explain blockdiag as it appears under T^2 in the Pooled statistics table:

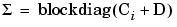, where C_iis the local covariance for test i, is calculated as shown below.

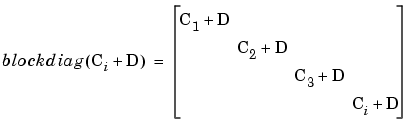
Linear Model Statistics Displays Design Evaluation Tool