| Model Browser User's Guide | |
Global Linear Models: Polynomials and Hybrid Splines
Polynomials
Polynomials of order n are of the form
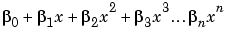
You can choose any order you like for each input factor.
As shown, a quadratic polynomial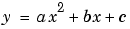 
can have a single turning point, and a cubic curve 
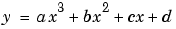can have two. As the order of a polynomial increases, it is possible to fit more and more turning points. The curves produced can have up to (n-1) bends for polynomials of order n.
Term Editor
Click the Edit Terms button to see the terms in the model. This opens the Term Editor dialog. Here you can remove any of the terms (see example).
See also Interaction.
Hybrid Splines
You can use the Hybrid Spline model to fit a spline to one factor and polynomials to all other factors.
A spline is a piecewise polynomial function, where different sections of polynomials are fitted smoothly together. The locations of the breaks are called knots. You can choose the required number of knots (up to a maximum of 50) and their positions. In this case all the pieces of curves between the knots are formed from polynomials of the same order. You can choose the order (up to 3).
The example following illustrates the shape of a spline curve with one knot and third-order basis functions. The knot position is marked on the N axis.
You can fit more complicated curves using splines, so they can be useful for the factor you expect to behave in the most complex way. This allows you to model detailed fluctuations in the response for one factor, while simpler models are sufficient to describe the other factors. The following example clearly shows that the response (Blow_2 in this case) is quadratic in the Load (L) axis and much more complex in the RPM (N) axis.
You can choose the order of the polynomial for each factor and the factor to fit the spline to. The maximum order for each factor is cubic.
The following example shows the options available for the Hybrid Spline linear model subclass.
This example only shows one input factor. When there are more, you use the radio buttons to select which factor is modeled with a spline. Select the order for each factor in the edit boxes.
See also the other linear model subclass, Polynomials.
Interaction
You can choose the interaction level on both linear model subclasses (polynomial and hybrid spline). For polynomials, the maximum interaction level is the same as the polynomial order (for example, 3 for cubics). For hybrid splines, the maximum interaction level is one less than the maximum order of the polynomials.
The interaction level determines the allowed order of cross-terms included.
You can use the Term Editor to see the effects of changing the interaction level. Click the Edit Terms button. The number of constant, linear, second- and third-order (and above) terms can be seen in the Model Terms frame.
For polynomials:. With an interaction level of 1, there are no terms in the model involving more than one factor. For example, for a four-factor cubic, for factor L, you see the terms for L,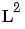 
, and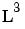 
, but no terms involving L and other factors. In other words, there are no cross-terms included.
If you increase the interaction level to 2, under second-order terms you see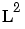 
and also L multiplied by each of the other factors; that is, second-order cross-terms (for example, LN, LA, and LS).
Increase the interaction to 3, and under third-order terms you see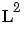 
multiplied by each of the other factors (
, 
, 
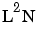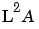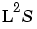), L multiplied by other pairs of factors (LNA, LNS, LAS), and L multiplied by each of the other factors squared (
, 
, 
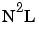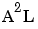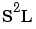). Interaction level 3 includes all third-order cross-terms.
The preceding also applies to all four factors in the model, not just L.
For hybrid splines:. The interaction function is different: it refers only to cross-term interactions between the spline term and the other variables. For example, at interaction order 1, raw spline terms only; interaction 1, raw terms and the spline terms x the first-order terms; interaction 3, includes spline terms x the second-order terms; and so on.
Stepwise
Take care not to overfit the data; that is, you do not want to use unnecessarily complex models that "chase points" in an attempt to model random effects.
The Stepwise feature can help.
Predicted sum of squares error(PRESS) is a measure of the predictive quality of a model.
Min PRESS throws away terms in the model to improve its predictive quality, removing those terms that reduce the PRESS of the model.
For a further discussion of the statistical effects of all the menu items in the Stepwise feature, see Stepwise Regression Techniques and Linear Model Statistics Displays.
| | Global Model Setup | Global Model Class: Radial Basis Function | |
