GARCH Toolbox

Conventions and Clarifications

Rows, Columns, Length, and Size

MATLAB operates as a large-scale, array-based processor, which makes it ideally suited for time series modeling and analysis. This manual imparts specific meanings to the words length and size in discussing arrays.

Matrices.   A matrix is an m-by-n array in which m is the number of rows and n is the number of columns. By convention, the rows (i.e., the m-dimension) of a time series matrix correspond to a time index. In any given column, the first row contains the oldest observation and the last row contains the most recent observation. Columns (i.e., the n-dimension) correspond to sample paths, independent realizations, or individual time series.

Let A be a 100-by-5 time series matrix generated to support a Monte Carlo simulation experiment. In this case, A has 100 observations for each of five independent sample paths (or equivalently, five realizations of some underlying univariate random process in which each column is a realization of an individual time series). In this case, the size of A is 100-by-5. If some other matrix, B, is the same size as A, then B is also a 100-by-5 matrix.

Since the current release of the GARCH Toolbox addresses univariate models only, matrices usually represent multiple realizations of a univariate time series (as opposed to a single realization of a multivariate time series). Whenever a GARCH Toolbox function detects the presence of an input matrix of size m-by-n, it assumes that m is the number of time-tagged observations and n is the number of realizations.

Vectors.   The length of a time series vector represents only the number of observations the vector contains. It does not indicate whether the vector is a row or column vector, i.e. it does not indicate the vector's size. For example, a time series vector of length 10 can be a row vector (i.e., a 1-by-10 matrix) or a column vector (i.e., a 10-by-1 matrix).

When a function detects a time series vector, row or column, it assumes that the vector represents a single realization of a univariate time series, and the length of the vector is the number of observations.

Note    Although most functions can process either row or column vectors, you can avoid confusing input/output arguments if you format single realizations of a univariate time series as column vectors. Using column vectors also makes it easier for you to display data in the MATLAB command window.

Precision

The GARCH Toolbox performs all its calculations in double precision. Select File > Preferences... > General > Numeric Format to set the numeric format for your displays. The default is Short.

Prices, Returns, and Compounding

The GARCH Toolbox assumes that time series vectors and matrices are time-tagged series of observations. If you have a price series, the toolbox lets you convert it to a return series using either continuous compounding or periodic compounding in accord with Eq. (2-10) and Eq. (2-11).

If you denote successive price observations made at time t and t+1 as P_t and P_t+1, respectively, continuous compounding transforms a price series {P_t} into a return series {y_t} as

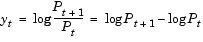
(2-10)

Periodic compounding defines the transformation as

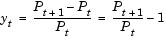
(2-11)

Continuous compounding is the default compounding method of the GARCH Toolbox, and is the preferred method for most of continuous-time finance. Since GARCH modeling is typically based on relatively high frequency data (i.e., daily or weekly observations), the difference between the two methods is usually small. However, there are some toolbox functions whose results are approximations for periodic compounding, but exact for continuous compounding. If you adopt the continuous compounding default convention when moving between prices and returns, all toolbox functions produce exact results.

Stationary and Nonstationary Time Series

Figure 2-3, Typical Equity Price Series illustrates a typical equity price series. Notice that there appears to be no long-run average level about which the series evolves. This is evidence of a nonstationary time series.

Figure 2-3: Typical Equity Price Series

Figure 2-4, Continuously Compounded Returns Associated with the Price Series, however, illustrates the continuously compounded returns associated with the same price series. In contrast, the returns appear to be quite stable over time, and the transformation from prices to returns has produced a stationary time series.

Figure 2-4: Continuously Compounded Returns Associated with the Price Series

The GARCH Toolbox assumes that return series are stationary processes. This may seem limiting, but the price-to-return transformation is common and generally guarantees a stable data set for GARCH modeling.

Models for the Conditional Mean and Variance

The Default Model