Fuzzy Logic Toolbox

Logical Operations

We now know what's fuzzy about fuzzy logic, but what about the logic?

The most important thing to realize about fuzzy logical reasoning is the fact that it is a superset of standard Boolean logic. In other words, if we keep the fuzzy values at their extremes of 1 (completely true), and 0 (completely false), standard logical operations will hold. As an example, consider the standard truth tables below.

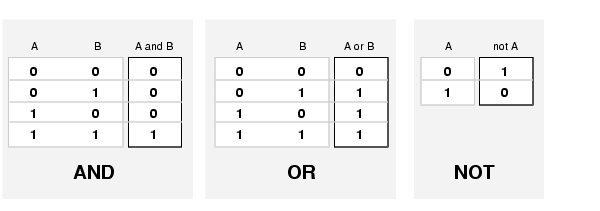
Now remembering that in fuzzy logic the truth of any statement is a matter of degree, how will these truth tables be altered? The input values can be real numbers between 0 and 1. What function will preserve the results of the AND truth table (for example) and also extend to all real numbers between 0 and 1?

One answer is the min operation. That is, resolve the statement A AND B, where A and B are limited to the range (0,1), by using the function min(A,B). Using the same reasoning, we can replace the OR operation with the max function, so that A OR B becomes equivalent to max(A,B). Finally, the operation NOT A becomes equivalent to the operation 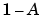. Notice how the truth table above is completely unchanged by this substitution.

Moreover, since there is a function behind the truth table rather than just the truth table itself, we can now consider values other than 1 and 0.

The next figure uses a graph to show the same information. We've converted the truth table to a plot of two fuzzy sets applied together to create one fuzzy set. The upper part of the figure displays plots corresponding to the two-valued truth tables above, while the lower part of the figure displays how the operations work over a continuously varying range of truth values A and B according to the fuzzy operations we've defined.

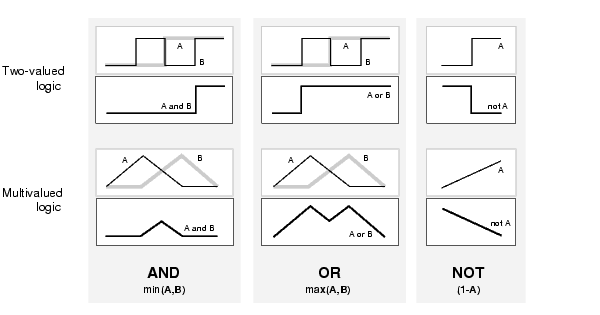
Given these three functions, we can resolve any construction using fuzzy sets and the fuzzy logical operation AND, OR, and NOT.

Additional Fuzzy Operators

We've only defined here one particular correspondence between two-valued and multivalued logical operations for AND, OR, and NOT. This correspondence is by no means unique.

In more general terms, we're defining what are known as the fuzzy intersection or conjunction (AND), fuzzy union or disjunction (OR), and fuzzy complement (NOT). We have defined above what we'll call the classical operators for these functions: AND = min, OR = max, and NOT = additive complement. Typically most fuzzy logic applications make use of these operations and leave it at that. In general, however, these functions are arbitrary to a surprising degree. The Fuzzy Logic Toolbox uses the classical operator for the fuzzy complement as shown above, but also enables you to customize the AND and OR operators.

The intersection of two fuzzy sets A and B is specified in general by a binary mapping T, which aggregates two membership functions as follows:

• µ_A«B(x) = T(µ_A(x), µ_B(x))

For example, the binary operator T may represent the multiplication of 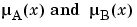. These fuzzy intersection operators, which are usually referred to as T-norm (Triangular norm) operators, meet the following basic requirements.

A T-norm operator is a binary mapping T(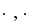) satisfying

• boundary: T(0, 0) = 0, T(a, 1) = T(1, a) = a

  monotonicity: T(a, b) <= T(c, d) if a <= c and b <= d

  commutativity: T(a, b) = T(b, a)

  associativity: T(a, T(b, c)) = T(T(a, b), c)

The first requirement imposes the correct generalization to crisp sets. The second requirement implies that a decrease in the membership values in A or B cannot produce an increase in the membership value in A intersection B. The third requirement indicates that the operator is indifferent to the order of the fuzzy sets to be combined. Finally, the fourth requirement allows us to take the intersection of any number of sets in any order of pairwise groupings.

Like fuzzy intersection, the fuzzy union operator is specified in general by a binary mapping S:

• µ_A»B(x) = S(µ_A(x), µ_B(x))

For example, the binary operator S can represent the addition of 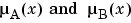. These fuzzy union operators, which are often referred to as T-conorm (or S-norm) operators, must satisfy the following basic requirements.

A T-conorm (or S-norm) operator is a binary mapping S(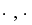) satisfying

• boundary: S(1, 1) = 1, S(a, 0) = S(0, a) = a

  monotonicity: S(a, b) <= S(c, d) if a <= c and b <= d

  commutativity: S(a, b) = S(b, a)

  associativity: S(a, S(b, c)) = S(S(a, b), c)

Several parameterized T-norms and dual T-conorms have been proposed in the past, such as those of Yager [Yag80], Dubois and Prade [Dub80], Schweizer and Sklar [Sch63], and Sugeno [Sug77]. Each of these provides a way to vary the "gain" on the function so that it can be very restrictive or very permissive.

Membership Functions

If-Then Rules