

| Fuzzy Logic Toolbox |   |
Membership Functions
A membership function (MF) is a curve that defines how each point in the input space is mapped to a membership value (or degree of membership) between 0 and 1. The input space is sometimes referred to as the universe of discourse, a fancy name for a simple concept.
One of the most commonly used examples of a fuzzy set is the set of tall people. In this case the universe of discourse is all potential heights, say from 3 feet to 9 feet, and the word "tall" would correspond to a curve that defines the degree to which any person is tall. If the set of tall people is given the well-defined (crisp) boundary of a classical set, we might say all people taller than 6 feet are officially considered tall. But such a distinction is clearly absurd. It may make sense to consider the set of all real numbers greater than 6 because numbers belong on an abstract plane, but when we want to talk about real people, it is unreasonable to call one person short and another one tall when they differ in height by the width of a hair.
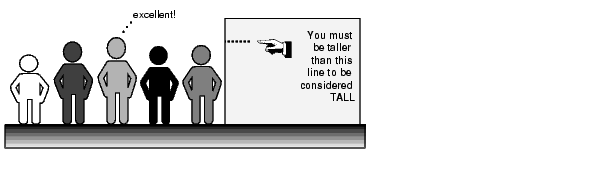
But if the kind of distinction shown above is unworkable, then what is the right way to define the set of tall people? Much as with our plot of weekend days, the figure following shows a smoothly varying curve that passes from not-tall to tall. The output-axis is a number known as the membership value between 0 and 1. The curve is known as a membership function and is often given the designation of µ. This curve defines the transition from not tall to tall. Both people are tall to some degree, but one is significantly less tall than the other.
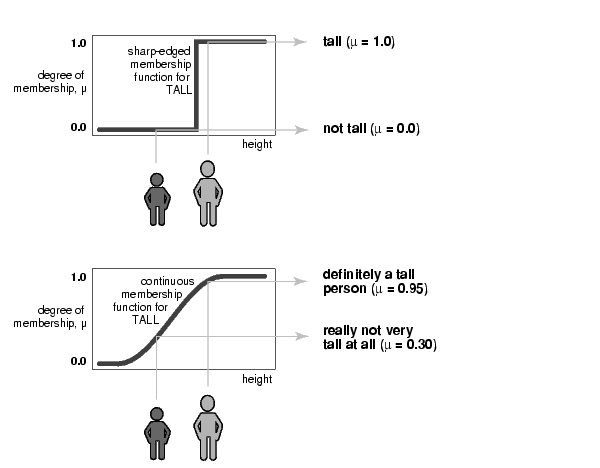
Subjective interpretations and appropriate units are built right into fuzzy sets. If I say "She's tall," the membership function "tall" should already take into account whether I'm referring to a six-year-old or a grown woman. Similarly, the units are included in the curve. Certainly it makes no sense to say "Is she tall in inches or in meters?"
Membership Functions in the Fuzzy Logic Toolbox
The only condition a membership function must really satisfy is that it must vary between 0 and 1. The function itself can be an arbitrary curve whose shape we can define as a function that suits us from the point of view of simplicity, convenience, speed, and efficiency.
A classical set might be expressed as
A fuzzy set is an extension of a classical set. If X is the universe of discourse and its elements are denoted by x, then a fuzzy set A in X is defined as a set of ordered pairs.
µA(x) is called the membership function (or MF) of x in A. The membership function maps each element of X to a membership value between 0 and 1.
The Fuzzy Logic Toolbox includes 11 built-in membership function types. These 11 functions are, in turn, built from several basic functions: piecewise linear functions, the Gaussian distribution function, the sigmoid curve, and quadratic and cubic polynomial curves. For detailed information on any of the membership functions mentioned below, turn to "Function Reference." By convention, all membership functions have the letters mf at the end of their names.
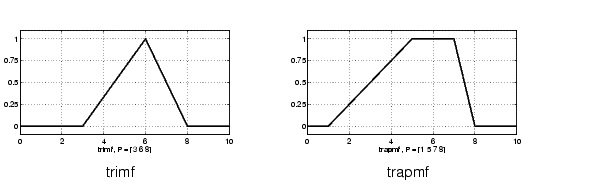
The simplest membership functions are formed using straight lines. Of these, the simplest is the triangular membership function, and it has the function name trimf. It's nothing more than a collection of three points forming a triangle. The trapezoidal membership function, trapmf, has a flat top and really is just a truncated triangle curve. These straight line membership functions have the advantage of simplicity.
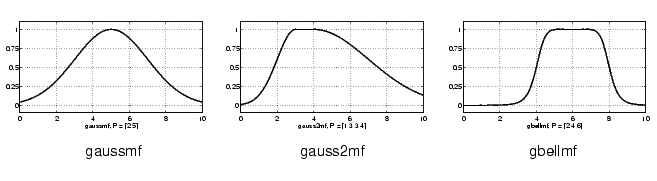
Two membership functions are built on the Gaussian distribution curve: a simple Gaussian curve and a two-sided composite of two different Gaussian curves. The two functions are gaussmf and gauss2mf.
The generalized bell membership function is specified by three parameters and has the function name gbellmf. The bell membership function has one more parameter than the Gaussian membership function, so it can approach a non-fuzzy set if the free parameter is tuned. Because of their smoothness and concise notation, Gaussian and bell membership functions are popular methods for specifying fuzzy sets. Both of these curves have the advantage of being smooth and nonzero at all points.
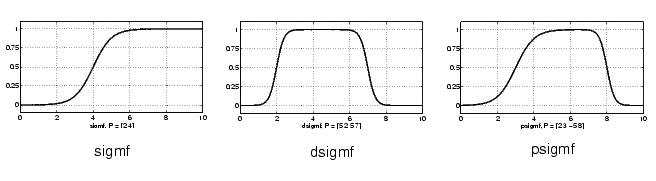
Although the Gaussian membership functions and bell membership functions achieve smoothness, they are unable to specify asymmetric membership functions, which are important in certain applications. Next we define the sigmoidal membership function, which is either open left or right. Asymmetric and closed (i.e. not open to the left or right) membership functions can be synthesized using two sigmoidal functions, so in addition to the basic sigmf, we also have the difference between two sigmoidal functions, dsigmf, and the product of two sigmoidal functions psigmf.
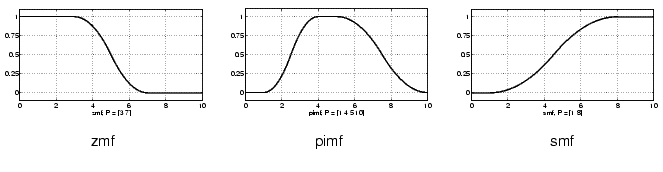
Polynomial based curves account for several of the membership functions in the toolbox. Three related membership functions are the Z, S, and Pi curves, all named because of their shape. The function zmf is the asymmetrical polynomial curve open to the left, smf is the mirror-image function that opens to the right, and pimf is zero on both extremes with a rise in the middle.
There's a very wide selection to choose from when you're selecting your favorite membership function. And the Fuzzy Logic Toolbox also allows you to create your own membership functions if you find this list too restrictive. On the other hand, if this list seems bewildering, just remember that you could probably get along very well with just one or two types of membership functions, for example the triangle and trapezoid functions. The selection is wide for those who want to explore the possibilities, but exotic membership functions are by no means required for perfectly good fuzzy inference systems. Finally, remember that more details are available on all these functions in the reference section, which makes up the second half of this manual.
Summary of Membership Functions
 | Foundations of Fuzzy Logic | Logical Operations |  |