Financial Derivatives Toolbox

Example: Fully Hedged Portfolio

Recall that hedgeopt allows you to allocate an optimal hedge by one of two goals:

• Minimize the cost of hedging a portfolio given a set of target sensitivities
• Minimize portfolio sensitivities for a given set of maximum target costs

As an example, reproduce the results for the fully hedged portfolio example.

• TargetSens = [0 0 0];
  FixedInd   = [1 4 5 7 8];
  [Sens,Cost,Quantity] = hedgeopt(Sensitivities, Price,... 
  Holdings, FixedInd, [], [], TargetSens);
  
  Sens =
  
           -0.00          -0.00          -0.00
  
  Cost =
  
        23055.90
  
  Quantity' =
  
           98.72
         -182.36
          -19.55
           80.00
            8.00
          -32.97
           40.00
           10.00 
  

This example finds a unique solution at a cost of just over $23,000. The matrix C (formed internally by hedgeopt and passed to lsqlin) is the asset Price vector expressed as a row vector.

• C = Price' = [98.72 97.53 0.05 98.72 100.55 6.28 0.05 3.69]
  

The vector d is the current portfolio value Value0 = 23674.62. The example maintains, as closely as possible, a constant portfolio value subject to the specified constraints.

Additional Constraints

In the absence of any additional constraints, the least squares objective involves a single equation with eight unknowns. This is an under-determined system of equations. Because such systems generally have an infinite number of solutions, you need to specify additional constraints to achieve a solution with practical significance. The additional constraints can come from two sources:

• User-specified equality constraints
• Target sensitivity equality constraints imposed by hedgeopt

The fully-hedged portfolio example specifies five equality constraints associated with holding assets 1, 4, 5, 7, and 8 fixed. This reduces the number of unknowns from eight to three, which is still an under-determined system. However, when combined with the first goal of hedgeopt, the equality constraints associated with the target sensitivities in TargetSens produce an additional system of three equations with three unknowns. This additional system guarantees that the weighted average of the delta, gamma, and vega of assets 2, 3, and 6, together with the remaining assets held fixed, satisfy the overall portfolio target sensitivity requirements in TargetSens.

Combining the least squares objective equation with the three portfolio sensitivity equations provides an overall system of four equations with three unknown asset holdings. This is no longer an under-determined system, and the solution is as shown.

If the assets held fixed are reduced, e.g., FixedInd = [1 4 5 7], hedgeopt returns a no cost, fully-hedged portfolio (Sens = [0 0 0] and Cost = 0).

If you further reduce FixedInd (e.g., [1 4 5], [1 4], or even []), hedgeopt always returns a no cost, fully-hedged portfolio. In these cases, insufficient constraints result in an under-determined system. Although hedgeopt identifies no cost, fully-hedged portfolios, there is nothing unique about them. These portfolios have little practical significance.

Constraints must be sufficient and appropriately defined. Additional constraints having no effect on the optimization are called dependent constraints. As a simple example, assume that parameter Z is constrained such that 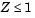. Furthermore, assume we somehow add another constraint that effectively restricts 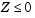. The constraint 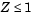now has no effect on the optimization.

Hedging with Constrained Portfolios

Example: Minimize Portfolio Sensitivities