DSP Blockset

LPC to LSF/LSP Conversion

Convert linear prediction coefficients (LPCs) to line spectral pairs (LSPs) or line spectral frequencies (LSFs)

Library

Estimation / Linear Prediction

Description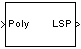

The LPC to LSF/LSP Conversion block takes a vector of linear prediction polynomial coefficients (LPCs) and converts it to a vector of line spectral pairs (LSPs) or line spectral frequencies (LSFs). When converting LPCs to LSFs, the block outputs match those of the poly2lsf function.

The input LPCs, 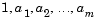, must be the denominator of the transfer function of a stable all-pole filter with the form given in Equation 7-5. A length-M+1 input yields a length-M output. Inputs can be sample- or frame-based vectors, but outputs are always sample-based vectors.

See other sections of this reference page to learn about how to ensure that you get valid outputs, how to detect invalid outputs, how the block computes the LSF/LSP values, and more.

Sections of This Reference Page

• Requirements for Getting Valid Outputs -- Requirements that the input LPCs and the Root finding coarse grid points parameter value must meet to ensure valid block outputs
• Setting Outputs to LSFs or LSPs -- Descriptions of three possible output formats you must select with the Output parameter
• Adjusting Output Computation Time and Accuracy with Root Finding Parameters -- How to adjust the block's root finding time and accuracy with the Root finding coarse grid points and Root finding bisection refinement parameters
• Valid Inputs and Corresponding Outputs -- Valid input frame statuses, sizes, and dimensions, and those of the corresponding output
• Handling and Recognizing Invalid Inputs and Outputs -- How to set block parameters for handling invalid inputs and outputs
• LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding -- Description and diagram of the block's root finding method
• Root Finding Method Limitations: Failure to Find Roots -- Description and diagram of how the block's root finding method can fail if parameters are not set properly
• Dialog Box -- A summary of the block parameters
• Supported Data Types -- Supported data types and a link to how to convert data types
• See Also -- Functions, blocks, and a paper related to the block

Requirements for Getting Valid Outputs

To get valid outputs, your inputs and the Root finding coarse grid points parameter value must meet these requirements:

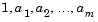• The input LPCs, , must come from the denominator of the following transfer function, H(z), of a stable all-pole filter (all roots of H(z) must be inside the unit circle). Note that the first term in H(z)'s denominator must be 1. If the input LPCs do not come from a transfer function of the following form, the block outputs are invalid.

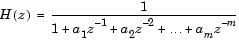
(7-5)

• The Root finding coarse grid points parameter value must be large enough so that the block can find all the LSP or LSF values. (The output LSFs and LSPs are roots of polynomials related to the input LPC polynomial; the block looks for these roots to produce the output. For details, see LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding.) If you do not set Root finding coarse grid points to a high enough value relative to the number of LPCs, the block may not find all the LSPs or LSFs and yield invalid outputs as described in Root Finding Method Limitations: Failure to Find Roots.

To learn about recognizing invalid inputs and outputs and parameters for dealing with them, see Handling and Recognizing Invalid Inputs and Outputs.

Setting Outputs to LSFs or LSPs

Set the Output parameter to one of the following settings to determine whether the block outputs LSFs or LSPs:

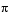• LSF in radians (0 pi) -- Block outputs the LSF values between 0 and radians in increasing order. The block does not output the guaranteed LSF values, 0 and .
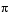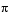• LSF normalized in range (0 0.5) -- Block outputs normalized LSF values in increasing order, computed by dividing the LSF values between 0 and radians by 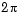. The block does not output the guaranteed normalized LSF values, 0 and 0.5.
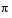• LSP in range (-1 1) -- Block outputs LSP values in decreasing order, equal to the cosine of the LSF values between 0 and radians. The block does not output the guaranteed LSP values, -1 and 1.

Adjusting Output Computation Time and Accuracy with Root Finding Parameters

The values 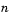 and 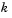 determine the block's output computation time and accuracy, where:

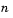• is the value of the Root finding coarse grid points parameter (choose this value with care; see the note below)
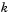• is the value of the Root finding bisection refinement parameter.
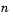• Decreasing the values of and 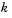decreases the output computation time, but also decreases output accuracy:
• The upper bound of block's computation time is proportional to .
• Each LSP output is within  of the actual LSP value.
• Each LSF output is within  of the actual LSF value, , where

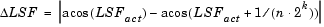
Note    If the value of the Root finding coarse grid points parameter is too small relative to the number of LPCs, the block may output invalid data as described in Requirements for Getting Valid Outputs. Also see Handling and Recognizing Invalid Inputs and Outputs.

Valid Inputs and Corresponding Outputs

The following list and table summarize characteristics of valid inputs and the corresponding outputs.

Notable Input and Output Properties.   

• To get valid outputs, your input LPCs and the value of the Root finding coarse grid points parameter must meet the requirements described in Requirements for Getting Valid Outputs.
• Block treats each column of an input matrix as a set of LPCs
• Length-L+1 input yields length-L output
• Output is always sample-based
• Output parameter determines the output type (see Setting Outputs to LSFs or LSPs):
• LSFs -- frequencies, , where and
• Normalized LSFs -- 
• LSPs -- 

Table 7-14: Input and Output Dimensions, Sizes, and Frame Statuses

Valid LPC Input	LSF and LSP Outputs (Always Sample-Based)
Sample-based length-M+1 row vector, Frame-based row vectors are not valid inputs.	Sample-based length-M row vector
Sample- or frame-based length-M+1 column vector,	Sample-based length-M column vector
1-D length-M+1 unoriented vector,	1-D length-M unoriented vector

Handling and Recognizing Invalid Inputs and Outputs

The block outputs invalid data if your input LPCs and the value of the Root finding coarse grid points parameter do not meet the requirements described in Requirements for Getting Valid Outputs. The following topics describe what invalid outputs look like, and how to set the block parameters provided for handling invalid inputs and outputs:

• What Invalid Outputs Look Like
• Parameters for Handling Invalid Inputs and Outputs

What Invalid Outputs Look Like.   Invalid outputs have the same dimensions, sizes, and frame statuses as valid outputs, which you can look up in Table 7-14, Input and Output Dimensions, Sizes, and Frame Statuses,. However, invalid outputs do not contain all the LSP or LSF values. Instead, invalid outputs contain none or some of the LSP and LSF values and the rest of the output vector or matrix is filled with place holder values (-1, 0.5, or 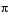 depending on the Output parameter setting).

In short, all invalid outputs end in one of the place holder values (-1, 0.5, or 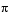) as illustrated in the following table. To learn how to use the block's parameters for handling invalid inputs and outputs, see the next section.

Output Parameter Setting	Place Holder	Example Invalid Outputs
LSF in radians (0 pi)
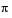LSF normalized in range (0 0.5)	0.5
LSP in range (-1 1)	-1

Parameters for Handling Invalid Inputs and Outputs.   You must set how the block handles invalid inputs and outputs by setting these parameters:

• Output validity of current output (1=valid, 0=invalid) -- Setting this parameter activates a second block output port that outputs a 1 when the output is valid, and a 0 when they are invalid. The LSF and LSP outputs are invalid if the block fails to find all the LSF or LSP values or if the input LPCs are unstable (for details, see Requirements for Getting Valid Outputs). See the previous section to learn how to recognize invalid outputs.
• If current output is invalid, overwrite with previous output -- Setting this parameter causes the block to overwrite invalid outputs with the previous output. If you set this parameter you also need to consider these parameters:
1. When first output is invalid, overwrite with user-defined values -- If the first input is unstable, you can choose to either overwrite the invalid first output with the default values (by clearing this parameter) or with values you specify (by setting this parameter and specifying the values in the parameter described next). The default initial overwrite values are the LSF or LSP representations of an all-pass filter.
2. User-defined LSP/LSF values for overwriting invalid first output -- In this parameter you specify the values for overwriting an invalid first output if you set the above parameter, When first output is invalid, overwrite with user-defined values. The vector of LSP/LSF values you specify should have the same dimension, size, and frame status as the other outputs, which you can look up in Table 7-14, Input and Output Dimensions, Sizes, and Frame Statuses,.
• If first coefficient of input not 1 -- The block output is invalid if the first coefficient in an LPC vector is not 1; this parameter determines what the block does when given such inputs:
• Ignore -- Proceed with computations as if the first coefficient is 1.
• Normalize -- Divide the input LPCs by the value of the first coefficient before computing the output.
• Normalize and warn -- In addition to Normalize, display a warning message at the MATLAB command line.
• Error -- Stop the simulation and display an error message at the MATLAB command line.

LSF and LSP Computation Method:
Chebyshev Polynomial Method for Root Finding

Note    To learn the principles on which the block's LSP and LSF computation method is based, see the reference listed in Reference.

To compute LSP outputs, the block relies on the fact that LSP values are the roots of two particular polynomials related to the input LPC polynomial; the block finds these roots using the Chebyshev polynomial root finding method, described next. To compute LSF outputs, the block computes the arccosine of the LSPs, outputting values ranging from 0 to 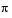radians.

Root Finding Method.   LSPs, which are the roots of two particular polynomials, always lie in the range (-1, 1). (The guaranteed roots at 1 and -1 are factored out.) The block finds the LSPs by looking for a sign change of the two polynomials' values between points in the range (-1, 1). The block searches a maximum of 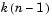 points, where

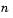• is the value of the Root finding coarse grid points parameter
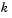• is the value of the Root finding bisection refinement parameter

The block's method for choosing which points to check consists of the following two steps:

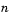1. Coarse Root Finding -- The block divides the interval [-1, 1] into intervals, each of length 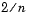, and checks the signs of both polynomials' values at the endpoints of the intervals. The block starts checking signs at 1, and continues checking signs at 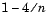, , 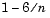and so on at steps of length 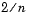, outputting any point if it is a root. The block stops searching in these situations:
• The block finds a sign change of a polynomial's values between two adjacent points. An interval containing a sign change is guaranteed to contain a root, so the block further searches the interval as described in Step 2, Root Finding Refinement.
• The block finds and outputs all M roots (given a length-M+1 LPC input)
• The block fails to find all M roots and yields invalid outputs as described in Handling and Recognizing Invalid Inputs and Outputs.
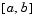2. Root Finding Refinement -- When the block finds a sign change in an interval, , it searches for the root guaranteed to lie in the interval by following these steps:
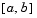1. Check if Midpoint Is a Root -- The block checks the sign of the midpoint of the interval . The block outputs the midpoint if it is a root, and continues Step 1, Coarse Root Finding, at the next point, 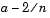. Otherwise, the block selects the half-interval with endpoints of opposite sign (eithe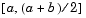r or 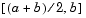) and executes Step b, Stop or Continue Root Finding Refinement.
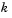2. Stop or Continue Root Finding Refinement -- If the block has repeated Step a   times ( 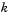is the value of the Root finding bisection refinement parameter), the block linearly interpolates the root by using the half-interval's endpoints, outputs the result as an LSP value, and returns to Step 1, Coarse Root Finding. Otherwise, the block repeats Step a using the half-interval.

   

Figure 7-13: Coarse Root Finding and Root Finding Refinement

Root Finding Method Limitations: Failure to Find Roots

The block root finding method described above can fail, causing the block to produce invalid outputs (for details on invalid outputs, see Handling and Recognizing Invalid Inputs and Outputs).

In particular, the block can fail to find some roots if the value of the Root finding coarse grid points parameter, 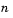, is too small. If the polynomials oscillate quickly and have roots that are very close together, the root finding may be too coarse to identify roots that are very close to each other, as illustrated in Figure 7-14, Fixing a Failed Root Finding,.

For higher-order input LPC polynomials, you should increase the Root finding coarse grid points value to ensure the block finds all the roots and produces valid outputs.

Figure 7-14: Fixing a Failed Root Finding

Dialog Box

Output

Specifies whether to convert the input linear prediction polynomial coefficients (LPCs) to LSP in range (-1 1), LSF in radians (0 pi), or LSF normalized in range (0 0.5). See Setting Outputs to LSFs or LSPs for descriptions of the three settings.

Root finding coarse grid points

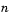The value , where the block divides the interval (-1, 1) into 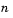subintervals of equal length, and looks for roots (LSP values) in each subinterval. You must pick  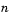large enough or the block output may be invalid as described in Requirements for Getting Valid Outputs. To learn how the block uses this parameter to compute the output, see LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding. Also see Adjusting Output Computation Time and Accuracy with Root Finding Parameters. Tunable.

Root finding bisection refinement

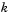The value , where each LSP output is within  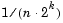of the actual LSP value, where 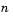is the value of the Root finding coarse grid points parameter. To learn how the block uses this parameter to compute the output, see LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding. Also see Adjusting Output Computation Time and Accuracy with Root Finding Parameters. Tunable.

Output the validity of current output (1=valid, 0=invalid)

Setting this parameter activates a second block output port that outputs a 1 when the output is valid, and a 0 when they are invalid. For more information, see Handling and Recognizing Invalid Inputs and Outputs.

If current output is invalid, overwrite with previous output

Setting this parameter causes the block to overwrite invalid outputs with the previous output. Setting this parameter activates other parameters for taking care of initial overwrite values (when the very first output of the block is invalid). For more information, see Parameters for Handling Invalid Inputs and Outputs.

When first output is invalid, overwrite with user-defined values

If the first input is unstable, you can choose to either overwrite the invalid first output with the default values (by clearing this parameter) or with values you specify (by setting this parameter). The default initial overwrite values are the LSF or LSP representations of an all-pass filter. For more information, see Parameters for Handling Invalid Inputs and Outputs.

User-defined LSP/LSF values for overwriting invalid first output

In this parameter you specify the values for overwriting an invalid first output if you set the parameter When first output is invalid, overwrite with user-defined values. The vector or matrix of LSP/LSF values you specify should have the same dimension, size, and frame status as the other outputs, which you can look up in Table 7-14, Input and Output Dimensions, Sizes, and Frame Statuses,.

If first coefficient of input not 1

Determines what the block does when the first coefficient of an input is not 1. The block can either proceed with computations as if the first coefficient is 1 (Ignore); divide the input LPCs by the value of the first coefficient before computing the output (Normalize); in addition to Normalize, display a warning message at the MATLAB command line (Normalize and warn); stop the simulation and display an error message at the MATLAB command line (Error). For more information, see Parameters for Handling Invalid Inputs and Outputs.

Supported Data Types

• Double-precision floating point
• Single-precision floating point
• Boolean -- Supported only by the optional output port that appears when you set the parameter, Output the validity of current output (1=valid, 0=invalid)

To learn how to convert to the above data types in MATLAB and Simulink, see Supported Data Types and How to Convert to Them.

Reference

Kabal, P. and Ramachandran, R. "The Computation of Line Spectral Frequencies Using Chebyshev Polynomials." IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. ASSP-34 No. 6, December 1986. pp. 1419-1426.

See Also

LSF/LSP to LPC Conversion	DSP Blockset
poly2lsf	Signal Processing Toolbox

Also see Linear Prediction for a list of all the blocks in the Linear Prediction library.

LMS Adaptive Filter

LSF/LSP to LPC Conversion