Curve Fitting Toolbox

Example: Nonparametric Fit

This example fits the following data using a cubic spline interpolant and several smoothing splines.

• rand('state',0);
  x = (4*pi)*[0 1 rand(1,25)]; 
  y = sin(x) + .2*(rand(size(x))-.5);
  

As shown below, you can fit the data with a cubic spline by selecting Interpolant from the Type of fit list.

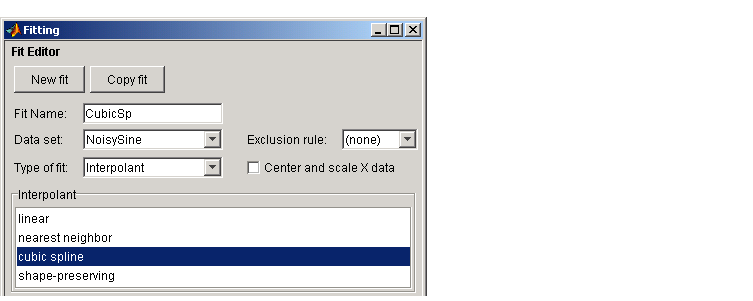
The results shown below indicate that goodness of fit statistics are not defined for interpolants.

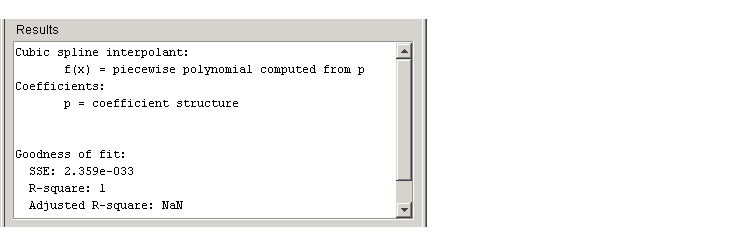
As described in Interpolants, cubic spline interpolation is defined as a piecewise polynomial that results in a structure of coefficients. The number of "pieces" in the structure is one less than the number of fitted data points, and the number of coefficients for each piece is four because the polynomial degree is three. The toolbox does not allow you to access the structure of coefficients.

As shown below, you can fit the data with a smoothing spline by selecting Smoothing Spline in the Type of fit list.

The level of smoothness is given by the Smoothing Parameter. The default smoothing parameter value depends on the data set, and is automatically calculated by the toolbox after you click the Apply button.

For this data set, the default smoothing parameter is close to 1, indicating that the smoothing spline is nearly cubic and comes very close to passing through each data point. Create a fit for the default smoothing parameter and name it Smooth1. If you do not like the level of smoothing produced by the default smoothing parameter, you can specify any value between 0 and 1. A value of 0 produces a piecewise linear polynomial fit, while a value of 1 produces a piecewise cubic polynomial fit, which passes through all the data points. For comparison purposes, create another smoothing spline fit using a smoothing parameter of 0.5 and name the fit Smooth2.

The numerical results for the smoothing spline fit Smooth1 are shown below.

The data and fits are shown below. The default abscissa scale was increased to show the fit behavior beyond the data limits. You change the axes limits with Tools->Axes Limit Control menu item.

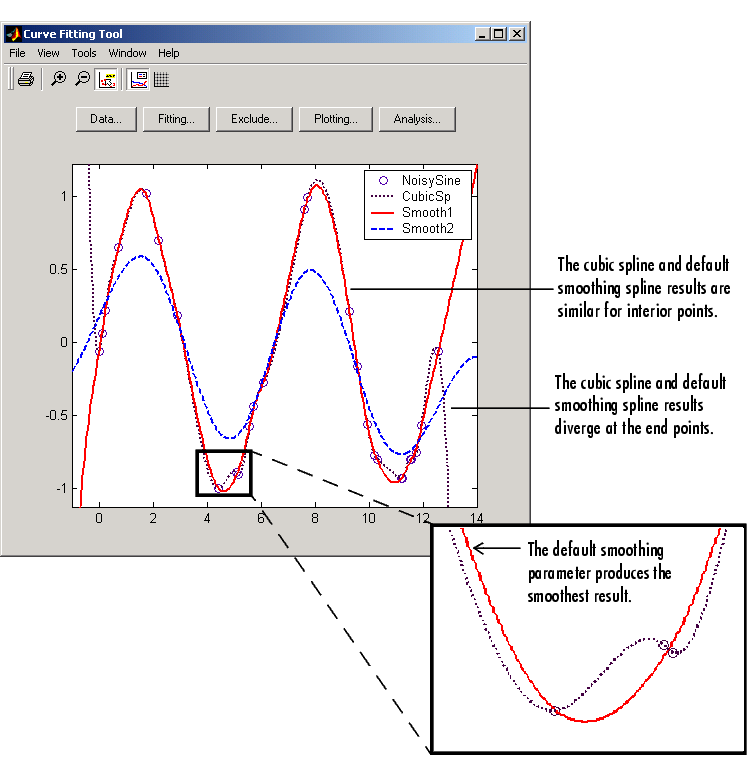
Note that the default smoothing parameter produces the smoothest curve. As the smoothing parameter increases beyond the default value, the associated curve approaches the cubic spline curve.

Smoothing Spline

Selected Bibliography