Curve Fitting Toolbox

Lowess and Loess: Local Regression Smoothing

The names "lowess" and "loess" are derived from the term "locally weighted scatter plot smooth," as both methods use locally weighted linear regression to smooth data.

The smoothing process is considered local because, like the moving average method, each smoothed value is determined by neighboring data points defined within the span. The process is weighted because a regression weight function is defined for the data points contained within the span. In addition to the regression weight function, you can use a robust weight function, which makes the process resistant to outliers. Finally, the methods are differentiated by the model used in the regression: lowess uses a linear polynomial, while loess uses a quadratic polynomial.

The local regression smoothing methods used by the Curve Fitting Toolbox follow these rules:

• The span can be even or odd.
• You can specify the span as a percentage of the total number of data points in the data set. For example, a span of 0.1 uses 10% of the data points.

The regression smoothing and robust smoothing procedures are described in detail below.

Local Regression Smoothing Procedure

The local regression smoothing process follows these steps for each data point:

1. Compute the regression weights for each data point in the span. The weights are given by the tricube function shown below.

1. 

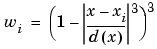
   x is the predictor value associated with the response value to be smoothed, x_i are the nearest neighbors of x as defined by the span, and d(x) is the distance along the abscissa from x to the most distant predictor value within the span. The weights have these characteristics:

   • The data point to be smoothed has the largest weight and the most influence on the fit.
   • Data points outside the span have zero weight and no influence on the fit.

2. A weighted linear least squares regression is performed. For lowess, the regression uses a first degree polynomial. For loess, the regression uses a second degree polynomial.
3. The smoothed value is given by the weighted regression at the predictor value of interest.

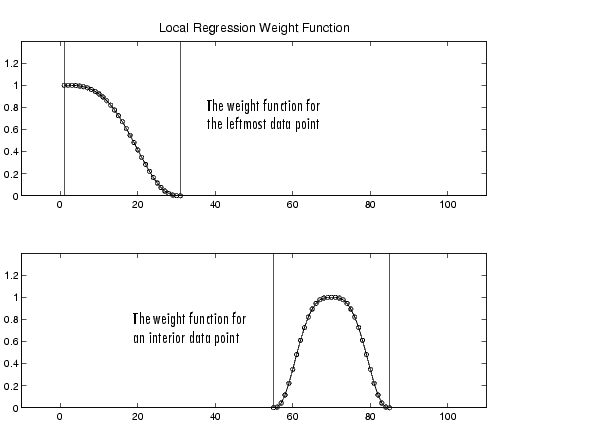
If the smooth calculation involves the same number of neighboring data points on either side of the smoothed data point, the weight function is symmetric. However, if the number of neighboring points is not symmetric about the smoothed data point, then the weight function is not symmetric. Note that unlike the moving average smoothing process, the span never changes. For example, when you smooth the data point with the smallest predictor value, the shape of the weight function is truncated by one half, the leftmost data point in the span has the largest weight, and all the neighboring points are to the right of the smoothed value.

The weight function for an end point and for an interior point is shown below for a span of 31 data points.

Using the lowess method with a span of five, the smoothed values and associated regressions for the first four data points of a generated data set are shown below.

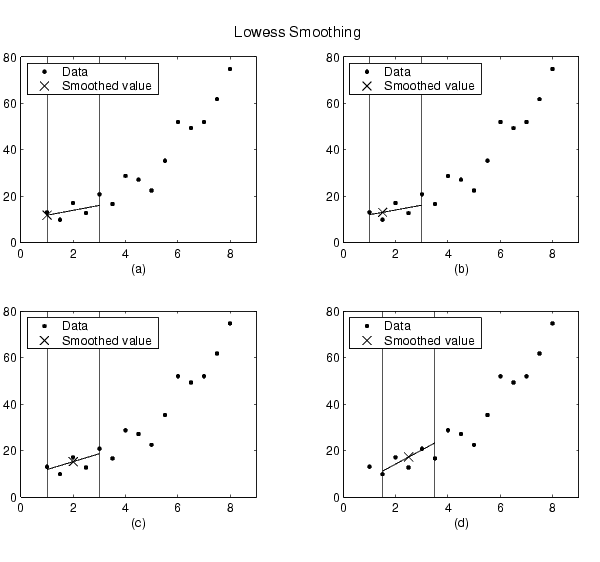
Notice that the span does not change as the smoothing process progresses from data point to data point. However, depending on the number of nearest neighbors, the regression weight function might not be symmetric about the data point to be smoothed. In particular, plots (a) and (b) use an asymmetric weight function, while plots (c) and (d) use a symmetric weight function.

For the loess method, the graphs would look the same except the smoothed value would be generated by a second-degree polynomial.

Robust Smoothing Procedure

If your data contains outliers, the smoothed values can become distorted, and not reflect the behavior of the bulk of the neighboring data points. To overcome this problem, you can smooth the data using a robust procedure that is not influenced by a small fraction of outliers. For a description of outliers, refer to Marking Outliers.

The Curve Fitting Toolbox provides a robust version for both the lowess and loess smoothing methods. These robust methods include an additional calculation of robust weights, which is resistant to outliers. The robust smoothing procedure follows these steps:

1. Calculate the residuals from the smoothing procedure described in the previous section.
2. Compute the robust weights for each data point in the span. The weights are given by the bisquare function shown below.

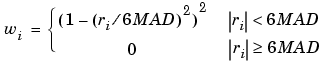
1. r_i is the residual of the ith data point produced by the regression smoothing procedure, and MAD is the median absolute deviation of the residuals:

1. The median absolute deviation is a measure of how spread out the residuals are. If r_i is small compared to 6MAD, then the robust weight is close to 1. If r_i is greater than 6MAD, the robust weight is 0 and the associated data point is excluded from the smooth calculation.

3. Smooth the data again using the robust weights. The final smoothed value is calculated using both the local regression weight and the robust weight.
4. Repeat the previous two steps for a total of five iterations.

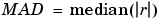
The smoothing results of the lowess procedure are compared below to the results of the robust lowess procedure for a generated data set that contains a single outlier. The span for both procedures is 11 data points.

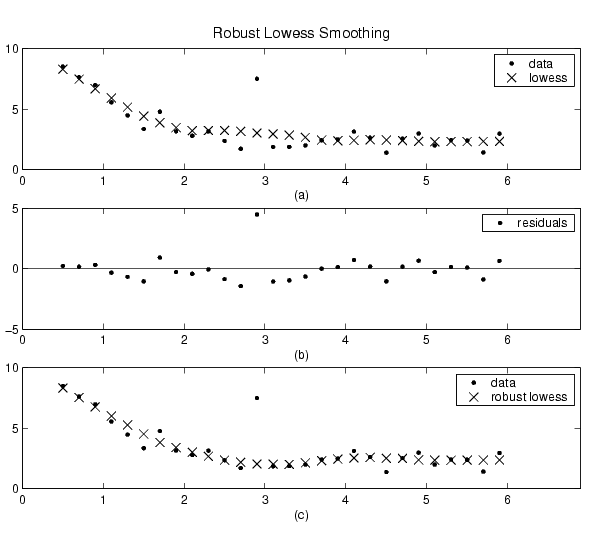
Plot (a) shows that the outlier influences the smoothed value for several nearest neighbors. Plot (b) suggests that the residual of the outlier is greater than six median absolute deviations. Therefore, the robust weight is zero for this data point. Plot (c) shows that the smoothed values neighboring the outlier reflect the bulk of the data.

Moving Average Filtering

Savitzky-Golay Filtering