Function Reference

feedback

Feedback connection of two LTI models

Syntax

• sys = feedback(sys1,sys2)
  sys = feedback(sys1,sys2,sign)
  sys = feedback(sys1,sys2,feedin,feedout,sign)
  

Description

sys = feedback(sys1,sys2) returns an LTI model sys for the negative feedback interconnection.

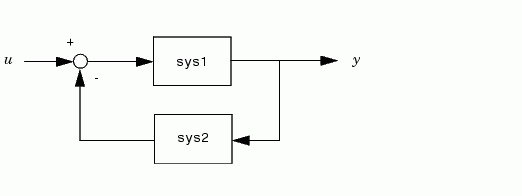
The closed-loop model sys has 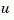as input vector and 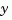as output vector. The LTI models sys1 and sys2 must be both continuous or both discrete with identical sample times. Precedence rules are used to determine the resulting model type (see Precedence Rules).

To apply positive feedback, use the syntax

• sys = feedback(sys1,sys2,+1)
  

By default, feedback(sys1,sys2) assumes negative feedback and is equivalent to feedback(sys1,sys2,-1).

Finally,

• sys = feedback(sys1,sys2,feedin,feedout)
  

computes a closed-loop model sys for the more general feedback loop.

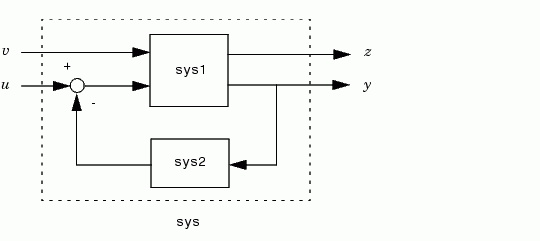
The vector feedin contains indices into the input vector of sys1 and specifies which inputs 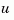are involved in the feedback loop. Similarly, feedout specifies which outputs 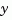of sys1 are used for feedback. The resulting LTI model sys has the same inputs and outputs as sys1 (with their order preserved). As before, negative feedback is applied by default and you must use

• sys = feedback(sys1,sys2,feedin,feedout,+1)
  

to apply positive feedback.

For more complicated feedback structures, use append and connect.

Remark

You can specify static gains as regular matrices, for example,

• sys = feedback(sys1,2)
  

However, at least one of the two arguments sys1 and sys2 should be an LTI object. For feedback loops involving two static gains k1 and k2, use the syntax

• sys = feedback(tf(k1),k2)
  

Examples

Example 1

To connect the plant

with the controller

using negative feedback, type

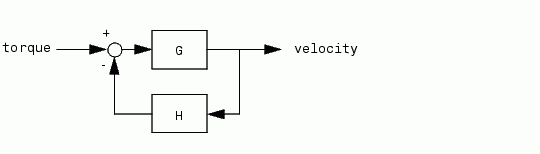
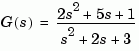
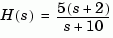
• G = tf([2 5 1],[1 2 3],'inputname','torque',...
                                'outputname','velocity');
  H = zpk(-2,-10,5)
  Cloop = feedback(G,H)
  

and MATLAB returns

• Zero/pole/gain from input "torque" to output "velocity":
  0.18182 (s+10) (s+2.281) (s+0.2192)
  -----------------------------------
   (s+3.419) (s^2 + 1.763s + 1.064)
  

The result is a zero-pole-gain model as expected from the precedence rules. Note that Cloop inherited the input and output names from G.

Example 2

Consider a state-space plant P with five inputs and four outputs and a state-space feedback controller K with three inputs and two outputs. To connect outputs 1, 3, and 4 of the plant to the controller inputs, and the controller outputs to inputs 4 and 2 of the plant, use

• feedin = [4 2];
  feedout = [1 3 4];
  Cloop = feedback(P,K,feedin,feedout)
  

Example 3

You can form the following negative-feedback loops

by

• Cloop = feedback(G,1)     % left diagram
  Cloop = feedback(1,G)     % right diagram
  

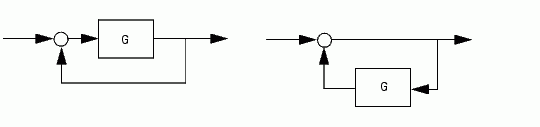
Limitations

The feedback connection should be free of algebraic loop. If 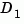and 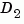are the feedthrough matrices of sys1 and sys2, this condition is equivalent to:

• nonsingular when using negative feedback
• nonsingular when using positive feedback.

See Also
series      Series connection

parallel    Parallel connection

connect     Derive state-space model for block diagram interconnection

evalfr

filt