

| Communications Blockset |   |
Apply a memoryless nonlinearity to a complex baseband signal.
Library
Description
The Memoryless Nonlinearity block applies a memoryless nonlinearity to a complex, baseband signal. You can use the block to model radio frequency (RF) impairments to a signal at the receiver.
The Memoryless Nonlinearity block provides five different methods for modeling the nonlinearity, which you specify by the Method parameter in the block's mask. The options for the Method parameter are
The five methods are implemented by subsystems underneath the block's mask. Each subsystem has the same basic structure, as shown in the figure below.
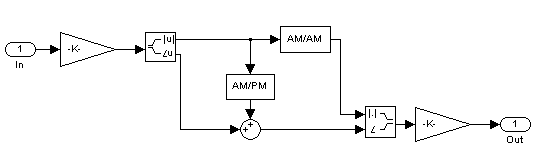
Figure 2-3: Nonlinearity Subsytem
All five subsystems apply a nonlinearity to the input signal as follows:
However, the subsystems implement the AM/AM and AM/PM conversions differently, according to the Method you specify.
If you want to see exactly how the Memoryless Nonlinearity block implements the conversions for a specific method, you can view the AM/AM and AM/PM subsystems that implement these conversions as follows:
The following figure shows, for the Saleh method, plots of
You can see the effect of the Memoryless Nonlinearity block on a signal modulated by 16-ary quadrature amplitude modulation (QAM) in a scatter plot. The constellation for 16-ary QAM without the effect of the Memoryless Nonlinearity block is shown in the following figure:
You can generate a scatter plot of the same signal after it passes through the Memoryless Nonlinearity block, with the Method parameter set to Saleh Model, as shown in the following figure.
This plot is generated by the model described in Scatter Plot Examples," with the following parameter settings for the Rectangular QAM Modulator Baseband block:
The following sections discuss parameters specific to the Saleh, Ghorbani, and Rapp models.
Parameters for the Saleh Model
The Input scaling (dB) parameter scales the input signal before the nonlinearity is applied. The block multiplies the input signal by the parameter value, converted from decibels to linear units. If you set the parameter to be the inverse of the input signal amplitude, the scaled signal has amplitude normalized to 1.
The AM/AM parameters, alpha and beta, are used to compute the amplitude gain for an input signal using the following function:
where u is the magnitude of the scaled signal.
The AM/PM parameters, alpha and beta, are used to compute the phase change for an input signal using the following function:
where u is the magnitude of the input signal. Note that the AM/AM and AM/PM parameters, although similarly named alpha and beta, are distinct.
The Output scaling (dB) parameter scales the output signal similarly.
Parameters for the Ghorbani Model
The Input scaling (dB) parameter scales the input signal before the nonlinearity is applied. The block multiplies the input signal by the parameter value, converted from decibels to linear units. If you set the parameter to be the inverse of the input signal amplitude, the scaled signal has amplitude normalized to 1.
The AM/AM parameters, [x1 x2 x3 x4], are used to compute the amplitude gain for an input signal using the following function:
where u is the magnitude of the scaled signal.
The AM/PM parameters, [y1 y2 y3 y4], are used to compute the phase change for an input signal using the following function:
where u is the magnitude of the input signal.
The Output scaling (dB) parameter scales the output signal similarly.
Parameters for the Rapp Model
The Smoothness factor and Output saturation level parameters are used to compute the amplitude gain for an input signal by the following function:
where S is the Smoothness factor and Osat is the Output saturation level.
The Rapp model does not apply a phase change to the input signal.
The Output saturation level parameter limits the output signal level.
Dialog Box
The following describes specific parameters for each method.
See Also
Reference
[1] Saleh, A.A.M., "Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers," IEEE Trans. Communications, vol. COM-29, pp.1715-1720, November 1981.
[2] A. Ghorbani, and M. Sheikhan, "The effect of Solid State Power Amplifiers (SSPAs) Nonlinearities on MPSK and M-QAM Signal Transmission", Sixth Int'l Conference on Digital Processing of Signals in Comm., 1991, pp. 193-197.
[3] C. Rapp, "Effects of HPA-Nonlinearity on a 4-DPSK/OFDM-Signal for a Digitial Sound Broadcasting System", in Proceedings of the Second European Conference on Satellite Communications, Liege, Belgium, Oct. 22-24, 1991, pp. 179-184.
 | M-DPSK Modulator Passband | M-FSK Demodulator Baseband |  |